Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Thế thì khi ta đứng trong tàu hoả đang chạy với tốc độ cao, sau khi nhảy lên, có phải ta cũng vẫn rơi xuống chỗ cũ như vậy chăng?
Có thể có người nghĩ như thế này: Tàu hoả đang chạy với tốc độ cao, trong quãng thời gian sau khi con người nhảy lên, tàu hoả đã chạy được một đoạn, con người phải rơi xuống ở chỗ lùi lại một ít. Tàu hoả chạy càng nhanh, khoảng cách so với chỗ cũ sau khi rơi xuống càng xa. Song sự thực cho chúng ta biết: Khi tàu hoả đang chạy với tốc độ cao, sau khi nhảy lên vẫn rơi đúng vào chỗ cũ. Vì sao lại như thế nhỉ?
Nguyên nhân là bất cứ vật thể nào cũng đều có quán tính. Chuyển động của vật thể phải tuân theo định luật quán tính. Nội dung của định luật quán tính (tức là định luật thứ nhất của Newton): Trong điều kiện không chịu tác động của ngoại lực, trạng thái chuyển động của vật thể sẽ không thay đổi. Khi tàu hoả đang chạy với tốc độ cao, cho dù con người đứng yên, nhưng trên thực tế người ấy đã lao về phía trước cùng với tàu hoả, với cùng một tốc độ như của tàu hoả. Khi người ấy nhảy lên, vẫn lao về phía trước cùng tàu hoả với cùng một tốc độ. Vì vậy, khi người ấy rơi xuống vẫn là chỗ cũ.
Đã từng có người nghĩ ra một ý “”tuyệt diệu””. Anh ta nói: chỉ cần tôi ngồi lên khí cầu bay lên cao, do sự tự quay của Trái Đất, tôi có thể trông thấy mặt đất ở phía dưới dịch chuyển nhanh chóng. Nếu bay lên từ Thượng Hải, dừng ở trên không khoảng một giờ rưỡi rồi lại hạ xuống, chẳng phải là đã đến thành La Sa của Khu tự trị Tây Tạng hay sao? Rõ ràng đó là chuyện không thể xảy ra. Vì rằng mọi vật xung quanh Trái Đất như con người, khí cầu, không khí… đều quay cùng Trái Đất mà!
Không nơi nào là không có quán tính. Khi một chiếc ô tô đang chạy rất nhanh, bỗng nhiên phanh gấp lại, người trong xe đều bị xô về phía trước, khi xe bỗng nhiên khởi động, người trong xe lại ngả về phía sau. Đó đều là do quán tính.”
Gọi S là quãng đường ô tô đi đến chỗ người đón.
\(S_1\) là khoảng cách chỗ người đó đang đứng đến nới ô tô đang đứng.
\(S_2\) là khoảng cách từ chỗ người đó đến quãng đường.
\(\Rightarrow S=\sqrt{S_1^2-S_2^2}=\sqrt{206^2-100^2}=6\sqrt{901}m\)
\(v=36\)km/h=10m/s
Thời gian ô tô đi đến chỗ đón:
\(t=\dfrac{S}{v}=\dfrac{6\sqrt{901}}{10}=18s\)
Vận tốc đi để vừa gặp ô tô là:
\(v'=\dfrac{S_1}{t}=\dfrac{100}{18}=5,55\)m/s
gọi
vị trí người đứng là: A
vị trí xe lúc đầu là: B
vị trí người gặp xe là :C
****************************
có:
AB=a=130m
AC=h=50m
BC=s1
v1=10m/s
t1=t2
v2=?
******
********giải********
S1=căn(a^2-b^2)=10*12=120(m)
t1=S1/v1=căn(a^2-h^2)/v1=120/10=12(s)
v2=h/t2=s2/t1= 50/12=25/6 (m/s)
Gọi S là quãng đường ô tô đi đến chỗ bạn An.
\(S_1\) là khoảng cách từ nơi bạn An đứng đến nơi ô tô đang đứng.
\(S_2\) là khoảng cách từ chỗ bạn An đến đường quốc lộ.
\(\Rightarrow S=\sqrt{S_1^2-S_2^2}=\sqrt{100^2-50^2}=50\sqrt{3}m\)
\(v=36\)km/h=10m/s
Thời gian ô tô đi đến chỗ bạn An:
\(t=\dfrac{S}{v}=\dfrac{50\sqrt{3}}{10}=5\sqrt{3}s\)
Vận tốc trung bình của An để vừa đón kịp xe:
\(v=\dfrac{S_1}{t}=\dfrac{100}{5\sqrt{3}}=\dfrac{20\sqrt{3}}{3}\approx11,55\)m/s
Giả sử người đó gặp ô tô tại điểm N. Khoảng thời gian t để người đó chạy từ M tới N phải đúng bằng khoảng thời gian để ô tô chạy từ A tới N
Ta có: AN = v 1 t = 36t
MN – v 2 t = 12t
Cả hai trường hợp, đều có H N 2 = M N 2 - h 2
Cuối cùng ta được phương trình bậc hai 1152 t 2 – 13,9428t + 0,04 = 0
Giải ra ta được hai nghiệm: t = 0,00743h ≈ 26,7 s hoặc t = 0,00467h ≈ 16,8 s
Do đó AN = 0,26748 km hoặc AN = 0,16812 km
Quãng đường MN mà người ấy phải chạy là MN = 89,2 m hoặc MN = 56 m
Gọi α là góc hợp bởi MN và MH:
Vậy người đấy có thể chạy theo hai hướng để bắt xe với các góc là 55 ° 54 ' hoặc 26 ° 46 '
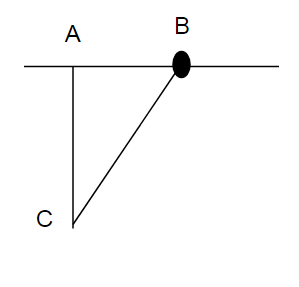
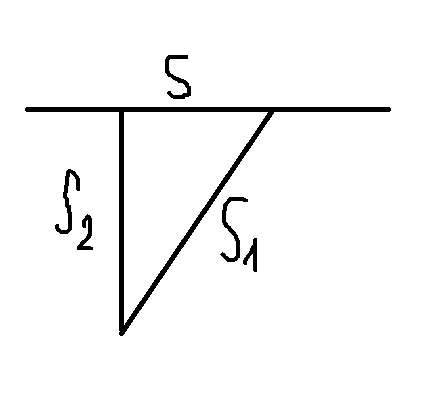
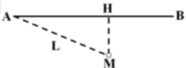
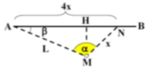
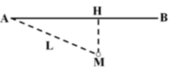
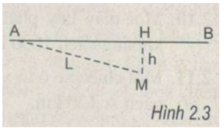
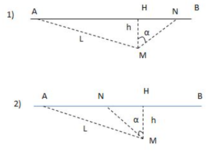
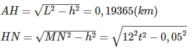
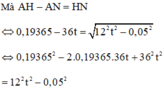
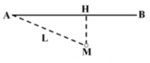
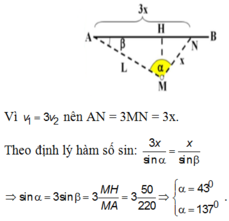
Cho AB là khoảng cách từ ô tô đến điểm gặp
AC là khoảng cách người đó tới điểm gặp ( mặt đường)
BC là khoảng cách của ô tô và người đó
Xét tam giác vuông ABC vuông tại A
Theo định lí py ta go ta có
AB2+AC2=BC2
=> AB=\(\sqrt{BC^2-AC^2}\)
=> AB =\(\sqrt{130^2-50^2}=120\left(m\right)\)
hay quãng đường ô tô phải đi để đến điểm gặp là 120(m)
Thời gian để cả 2 gặp nhau là:
t=\(\frac{s_{AB}}{v_{ôtô}}=\frac{120}{10}=12\left(s\right)\)
Vận tốc người đó phải đi là
v=\(\frac{s_{AC}}{t}=\frac{50}{12}=4.17\)(m/s)
Gọi \(S\) là quãng đường ô tô đi đến chỗ người đó đón
\(S_1\) là khoảng cách chỗ người đó đang đứng đến nới ô tô đang đứng
\(S_2\) là khoảng cách từ chỗ người đó đến quãng đường
\(S=\sqrt{S_1^2-S_2^2}=\sqrt{130^2-50^2}=120\left(m\right)\)
Thời gian ô tô đi đến chỗ đón là :
\(t=\dfrac{S}{V_1}=\dfrac{120}{10}=12\left(s\right)\)
Vận tốc ô tô chạy để có thể gặp ô tô là:
\(V_2=\dfrac{S_2}{t}=\dfrac{50}{12}=4,16\)(m/s)