Cho hình hộp ABCD.A'B'C'D'. Xét M thuộc BB', N thuộc Cd sao cho BM : MB' = CN : ND và gọi I, J theo thứ tự là trungd diểm BC, D'A'. Chứng minh rằng M, N, I, J đồng phẳng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
1 tháng 2 2019
Ta có:
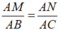
suy ra MN // BC (1) (Định lý Ta-lét đảo).
- Lại có: MN ∩ (MNI) (2)
- Từ (1) và (2) suy ra: BC // (MNI)

29 tháng 6 2017
a) ED là đường TB ⇒ED//BC⇒EDBC⇒ED//BC⇒EDBC là hbh
b) Ta có EM là đường TB của ΔABNΔABN
⇒EM//AN⇒EM//KN⇒EM//AN⇒EM//KN
Vì N là trung điểm MC ⇒K⇒K là trung điểm EC
c) C/m tương tự được I là trung điểm BD
Ta có OI=OB2OI=OB2 (O là giao điểm trung tuyến , quên đưa vào hình )
DI=3OB4DI=3OB4
OI=OB4OI=OB4
Chưng minh tương tự được OK=OC4OK=OC4
Vì OIOB=OKOC=14OIOB=OKOC=14
⇒IK//BC⇒IKBC=14
https://diendan.hocmai.vn/threads/toan-8-hinh-thang.496732/
Do \(\frac{BM}{MB'}=\frac{CN}{ND}\) nên \(\frac{BM}{BB'}=\frac{CN}{CD}=t\) với \(t\in\left(0;1\right)\) nào đó
Đặt \(\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AD}=\overrightarrow{b}\) và \(\overrightarrow{AA'}=\overrightarrow{c}\)
Khi đó :
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{a}+t\overrightarrow{c}\)
\(\overrightarrow{AN}=\overrightarrow{AD}+\overrightarrow{DN}=\left(1-t\right)\overrightarrow{a}+\overrightarrow{b}\)
\(\overrightarrow{AI}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}\)
\(=\overrightarrow{AA'}+\overrightarrow{A'J}=\frac{1}{2}\overrightarrow{b}+\overrightarrow{c}\)
Suy ra :
\(\overrightarrow{MN}=-t.\overrightarrow{a}+\overrightarrow{b}-t.\overrightarrow{c}\) ; \(\overrightarrow{MI}=\frac{1}{2}\overrightarrow{b}-t\overrightarrow{c}\) và \(\overrightarrow{MJ}=-\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}+\left(1-t\right).\overrightarrow{c}\)
Từ đó, do
\(-t.\overrightarrow{a}+\overrightarrow{b}-t.\overrightarrow{c}=\left(2-t\right).\left(\frac{1}{2}.\overrightarrow{b}-t.\overrightarrow{c}\right)+t.\left(-\overrightarrow{a}\right)+\frac{1}{2}.\overrightarrow{b}+\left(1-t\right).\overrightarrow{c}\)
Nên :
\(\overrightarrow{MN}=\left(2-t\right).\overrightarrow{MI}+t.\overrightarrow{MJ}\)
Suy ra M, N, I, J đồng phẳng