Cho hai đường tròn (O) và (O’) cắt nhau ở A và B (O và O’ thuộc 2 nửa mặt phẳng bờ AB).
Kẻ các đường kính BOC và BO’D. Biết OO’ = 10cm, OB = 8cm, O’B = 6cm.
Diện tích tam giác BCD là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3. pt có 2 nghiệm x1, x2, theo vi-ét: x1+x2=-m và x1x2=1/m
x1_^3+x2_^3=0
=>(x1+x2)(x1_^2+x2_^2-x1x2)=0
=>(x1+x2)((x1_^2+x2_^2)^2-3x1x2)=0
=>-m(m^2-3/m)=0
=>-m^3+3
=>m=-căn bậc 3 của 3

a: góc CAB=1/2*sđ cung CB=90 độ
góc BAD=1/2*sđ cung BD=90 độ
góc CAD=góc CAB+góc BAD
=90 độ+90 độ=180 độ
=>C,A,D thẳng hàng

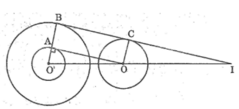
Xét tứ giác ABCO ta có:
AB // CO (gt) (1)
Mà : AB = O’B – O’A = 3 – 1 = 2 (cm)
Suy ra: AB = OC = 2 (cm) (2)
Từ (1) và (2) suy ra: ABCO là hình bình hành
Lại có: OA ⊥ O’A (tính chất tiếp tuyến)
Suy ra: BC ⊥ OC và BC ⊥ O’B
Vậy BC là tiếp tuyến chung của hai đường tròn (O) và (O’)

Mình sẽ giải lại 2 câu a và b.
a) Vì (O) và (O') giao nhau tại A và B nên AB vuông góc OO'. Do đó ^BO'O = 1/2.^AO'B = ^BDA
Tương tự ^BOO' = ^BCA. Từ đó \(\Delta\)BOO' ~ \(\Delta\)BCD (g.g) (đpcm).
b) Ta thấy: ^KDA = ^ABD (=1/2.Sđ(AD nhỏ của (O')). Tương tự ^KCA= ^ABC
Nên ta có: ^KCB + ^KDB = ^BCD + ^BDC + ^KDA + ^KCA = ^BDC + ^BCD + ^ABD + ^ABC = 1800
Suy ra tứ giác BCKD nội tiếp (đpcm).
c) Vì IE // DK nên ^DIE = ^KDA (So le trong) = ^ABD (cmt) => ^DIE = ^ABE => Tứ giác AIEB nội tiếp
=> ^BAE = ^BIE = ^BKD (Vì IE // KD) = ^BCD (Tứ giác BCKD nt) = 1/2.Sđ(AB nhỏ của (O)
Do vậy AE là tiếp tuyến của (O) (đpcm).