Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có dây đàn hồi được treo lơ lửng trên một cần rung như vậy ứng với sóng dừng một đầu cố định một đầu tự do
khi đó
l
=
(
2
k
+
1
)
λ
4
=
(
2
k
+
1
)
v
4
f
⇒
f
=
(
2
k
+
1
)
v
4
l
=
2
(
2
k
+
1
)
100 ≤ f ≤ 120 ⇒ 24 , 5 ≤ k ≤ 29 , 5
⇒
Có 5 giá trị k thoả mãn
Như vậy có thể tạo được 5 lần sóng dừng trên dây khi thay đổi tần số rung của cần

Đáp án B
Gọi tần số ban đầu là f1. Ta có AB = k λ 1 2 = k v 2 f 1 (số nút là k + 1)
Tần số sau khi tăng là f 2 = f 1 + 30 thì số nút sóng tăng thêm 5 nút.
Ta có:
AB = (k+5) λ 2 2 = ( k + 5 ) v 2 ( f 1 + 30 ) ⇒ f 1 = 6 k ⇒ A B = v 12 = 1 m ⇒ v = 12 m/s.

Chọn đáp án C
Gọi tần số ban đầu là f 1 . Ta có A B = k λ 1 2 = k v 2 f 1 (số nút là k + 1)
Tần số sau khi tăng là f 2 = f 1 + 30 thì số nút sóng tăng thêm 5 nút.
Ta có:
A B = ( k + 5 ) λ 2 2 = ( k + 5 ) v 2 ( f 1 + 30 )
⇒ f 1 = 6 k ⇒ A B = v 12 = 1 m ⇒ v = 12 m/s.

Đáp án B
Sóng dừng với một đầu nút, một đầu bụng là
l = 2 k + 1 λ 4 = 2 k + 1 v 4 f ⇒ f = 2 k + 1 v 4 l = 2 k + 1 10 4.0,8 = 2 k + 1 3,125
Mà 50 ≤ 2 k + 1 3,125 ≤ 80 ⇔ 7,5 ≤ k ≤ 12,3 ⇒ k = 8,9,10,11,12.
Có 5 giá trị tần số cho sóng dừng trên dây

Đáp án B
Sóng dừng với một đầu nút, một đầu bụng là
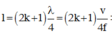
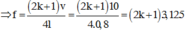
Mà
![]()
Có 5 giá trị tần số cho sóng dừng trên dây.



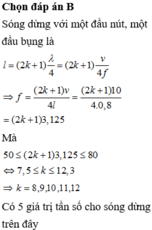
Bước sóng: \(\lambda=\frac{v}{f}=0,12m=12cm\)
Với 1 đầu thả lỏng, khi sóng dừng được tạo ra thì đầu thả lỏng là 1 bụng sóng.
Chiều dài dây là L. Ta có:\(L=k\frac{\lambda}{2}+\frac{\lambda}{4}=\left(k+\frac{1}{2}\right)\frac{\lambda}{2}=6\left(k+\frac{1}{2}\right)\left(cm\right)\)
Với L từ 24cm đến 120cm, ta có k từ 3,5 đến 19,5
\(\text{3,5≤k≤19,5}\)
Vậy k nhận các giá trị: k=4, k=5, k=6, ....., k=19
Tất cả có 16 giá trị ứng với 16 lần có sóng dừng.
Đáp án C.
trả hiểu gì
ai giải thích lại được ko??????????????