Một bánh đà đang quay quanh trục với vận tốc góc 300 vòng/phút thì quay chậm lại vì có ma sát với ổ trục. Sau một giây, vận tốc chỉ còn bằng 0,9 vận tốc ban đầu.
Tính vận tốc sau giây thứ hai, coi ma sát là không đổi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
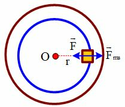
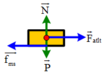
Vật m không trượt lên đĩa quay khi lực ma sát F m s → giữa vật và đĩa lớn hơn hoặc bằng lực F → (lực gây ra gia tôc hướng tâm cho vật): F m s → ≥ F
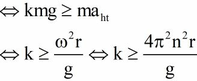

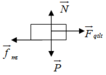
Ta có ω = 30. 2 π 60 = π r a d / s
Để vật không bị trượt ra khỏi bàn: F q t l t ≤ F m s
⇒ m ω 2 . r ≤ μ . N = μ . m . g
⇒ μ ≥ ω 2 . r g = π 2 .0 , 2 10 = 0 , 2

+ Xét tại điểm B:
Vận tốc góc vật: \(\omega=\dfrac{v_B}{r_B}=\dfrac{0,5}{0,12}=\dfrac{25}{6}\)(rad/s)
+Xét tại điểm A:
Bán kính với A là: \(r_A=\dfrac{v_A}{\omega}=\dfrac{0,8}{\dfrac{25}{6}}=0,192\)(m/s)
Bạn ơi mình thắc mắc tính là sao tốc độ góc bằng nhau được vậy ạ? Tại mình thấy v khác nhau mà nhỉ?

Lực tác dụng lên sàn: \(F=350N\)
Cánh tay đòn của vật: \(R=0,45m\)
Momen quán tính:
\(I=\dfrac{1}{2}mR^2=\dfrac{1}{2}\cdot80\cdot0,45^2=8,1kg.m^2\)
Mà \(M=F\cdot R=I\cdot\gamma\)
Gia tốc góc của sàn \(\gamma\):
\(\gamma=\dfrac{F\cdot R}{I}=\dfrac{350\cdot0,45}{8,1}=19,44\)(rad/s2)
Vận tốc góc của sàn tại \(t=50s\) là:
\(\omega=\omega_0+\gamma t=0+19,44\cdot50=972,22\)(rad/s)

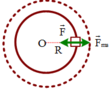


Vận tốc ban đầu là 300 vòng/phút tương ứng với \(\omega_0=10\pi\) rad/s
Trong giây đầu tiên vận tốc chỉ còn 0.9 vận tốc ban đầu nghĩa là còn 9\(\pi\) rad/s
suy ra \(\gamma=-\pi\) rad/s2
Vận tốc sau giây thứ 2 sẽ còn là \(8\pi\) rad/s