Một bánh xe quay được 180 vòng trong 30s. Tốc độ góc của nó lúc cuối thời gian trên là 10 vòng/s. Giả sử bánh xe đã được tăng tốc với gia tốc không đổi.Hỏi:
a) Tốc độ lúc bắt đầu đếm số vòng.
b) Thời gian quay từ lúc nghỉ ban đầu đến lúc đạt được tốc độ đó.
c) Phương trình chuyển động của bánh xe. Lấy gốc thời gian là lúc nó bắt đầu quay từ trạng thái nghỉ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

VT
21 tháng 11 2017
Chọn đáp án A
+ Áp dụng công thức:![]()
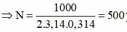 vòng
vòng
Vậy thời gian quay hết một vòng
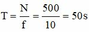

CT
27 tháng 10 2021
Ta có:
+ Chu kì quay của bánh xe:
+ Tần số:
+ Tốc độ góc:
+ Tốc độ dài của một điểm trên vành bánh xe:

9 tháng 10 2021
1.Bánh xe quay đều 100 vòng trong thời gian 2s\(\Rightarrow\) \(f=\dfrac{2}{100}=0,02\)vòng/s
Tần số quay của bánh xe: \(f=50\) vòng/s
Chu kì quay: \(T=\dfrac{1}{f}=\dfrac{1}{50}s\)
2.Vận tốc góc của 1 điểm trên vành bánh xe: \(\omega=\dfrac{2\pi}{T}=100\pi\) rad/s
Vận tốc dài của 1 điểm trên vành bánh xe: \(v=\omega.r=100\pi.0,6=60\pi\) m/s
3. Gia tốc hướng tâm của 1 điểm trên vành bánh xe:
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(60\pi\right)^2}{0,6}\approx59217,63\) m/s2
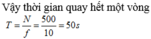

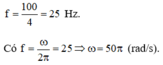
Theo công thức của chuyển động quay biến đổi đều
\(\omega^2-\omega^2_0=2.\gamma.\varphi\)
\(\left(\omega-\omega_0\right).\left(\omega+\omega_0\right)=2.\frac{\left(\omega-\omega_0\right)}{t}.\varphi\)
\(\left(\omega+\omega_0\right).t=2.\varphi\)
Với \(t=30s\), \(\omega=20\pi\) và \(\varphi=360\pi\)
suy ra
\(\omega_0=4.\pi\) rad/s và \(\gamma=16\pi\text{ /}30\) rad/s2
Thời gian để đạt được tốc độ \(\omega_0\) từ trạng thái nghỉ là \(\omega_0\text{π /}\gamma\) = 7.5 s
Phương trình chuyển động của bánh xe từ trạng thái nghỉ là
\(\varphi\)= (1/2 ). (16\(\pi\)/30).t2 rad
Dạng toán này giờ không còn học nữa mà