khi giải phương trình và hệ phương trình thì có được phép rút gọn hay không, trường hợp nào sẽ bị bị mất nghiệm và quy đồng có được bỏ mẫu không?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta gọi 5 tên cướp biển là A, B, C, D, E (từ giá nhất đến trẻ nhất). Ta giải ngược từ dưới lên như sau.
Nếu chỉ có 2 tên cướp biển: D chia số tiền theo tỷ lệ 100:0 (lấy hết số tiền vàng về mình). Anh ta sẽ biểu quyết đồng ý và điều này đủ để phương án được thông qua.
Nếu chỉ có 3 tên cướp biển: C sẽ chia số tiền theo tỷ lệ 99 : 0 : 1. E sẽ chấp nhận phương án này (chỉ được có 1 đồng vàng), vì anh ta biết rằng trong trường hợp anh ta phản đối phương án, chỉ còn lại D và E thì anh ta sẽ chẳng được gì.
Nếu có 4 cướp biển: B chia tiền thành 99: 0 : 1: 0. Cũng lý luận như trên, ta thấy D sẽ ủng hộ phương án này. B cũng không nên dùng 1 đồng để mua chuộc C vì C biết rằng nếu anh ta không ủ hộ B, anh ta sẽ bỏ túi 99 đồng xu nếu B bị vứt xuống biển. B cũng không nên mua chuộc E vì E biết rằng nếu B bị vứt xuống biển và C chia tiền thì anh ta cũng sẽ được C chia cho 1 đồng.
Nếu có 5 cướp biển: A chia các đồng tiền theo tỷ lệ 98 : 0 : 1 : 0 : 1. Bằng cách cho C và E mỗi người một đồng tiền vàng (những người sẽ chẳng được gì nếu không đồng ý phương án của A), anh ta đảm bảo phương án sẽ được thông qua.
Ghi chú: Trong trường hợp cuối (cũng chính là trường hợp của đề bài) A không cho B tiền vì B biết rằng nếu anh ta không đồng ý phương án của A và A bị vứt xuống biển thì anh ta sẽ bỏ túi 99 đồng. Tương tự như vậy, anh ta sẽ không cho D một đồng tiền vàng, vì D biết nếu A thất bại thì B cũng cho D một đồng tiền vàng như A. Mà như thế thì do tính khát máu, D sẽ không bỏ phiếu cho A.

Khi biến đổi phương trình mà làm mất mẫu chứa ẩn của phương trình thì phương trình nhận được:
A . luôn không tương đương với phương trình ban đầu
B . có thể không tương đương với phương trình ban đầu
C. luôn tương đương với phương trình ban đầu

Khi a và c trái dấu thì ac < 0, suy ra –ac > 0, suy ra -4ac > 0
Ta có: ∆ = b 2 – 4ac, trong đó b 2 > 0
Nếu -4ac > 0 thì ∆ luôn lớn hơn 0.
Khi ∆ > 0 nghĩa là phương trình có hai nghiệm phân biệt.
Áp dụng :
2010 x 2 + 5x - m 2 = 0 (1)
*Với m = 0 thì (1) ⇔ 2010 x 2 + 5x = 0: phương trình có 2 nghiệm.
*Với m ≠ 0 ta có: m 2 > 0, suy ra: - m 2 < 0
Vì a = 2010 > 0, c = - m 2 < 0 nên ac < 0
Vậy phương trình (1) có 2 nghiệm phân biệt.

Khi a và c trái dấu thì ac < 0, suy ra –ac > 0, suy ra -4ac > 0
Ta có: ∆ = b 2 – 4ac, trong đó b 2 > 0
Nếu -4ac > 0 thì ∆ luôn lớn hơn 0.
Khi ∆ > 0 nghĩa là phương trình có hai nghiệm phân biệt.
Áp dụng :
Phương trình 3 x 2 – x – 8 = 0 có:
a = 3, c = -8 nên ac < 0
Vậy phương trình có 2 nghiệm phân biệt.

Khi a và c trái dấu thì ac < 0, suy ra –ac > 0, suy ra -4ac > 0
Ta có: ∆ = b 2 – 4ac, trong đó b 2 > 0
Nếu -4ac > 0 thì ∆ luôn lớn hơn 0.
Khi ∆ > 0 nghĩa là phương trình có hai nghiệm phân biệt.
Áp dụng :
Phương trình 2004 x 2 + 2x - 1185 5 = 0 có:
a = 2004, c = -1185 5 nên ac < 0
Vậy phương trình có 2 nghiệm phân biệt.
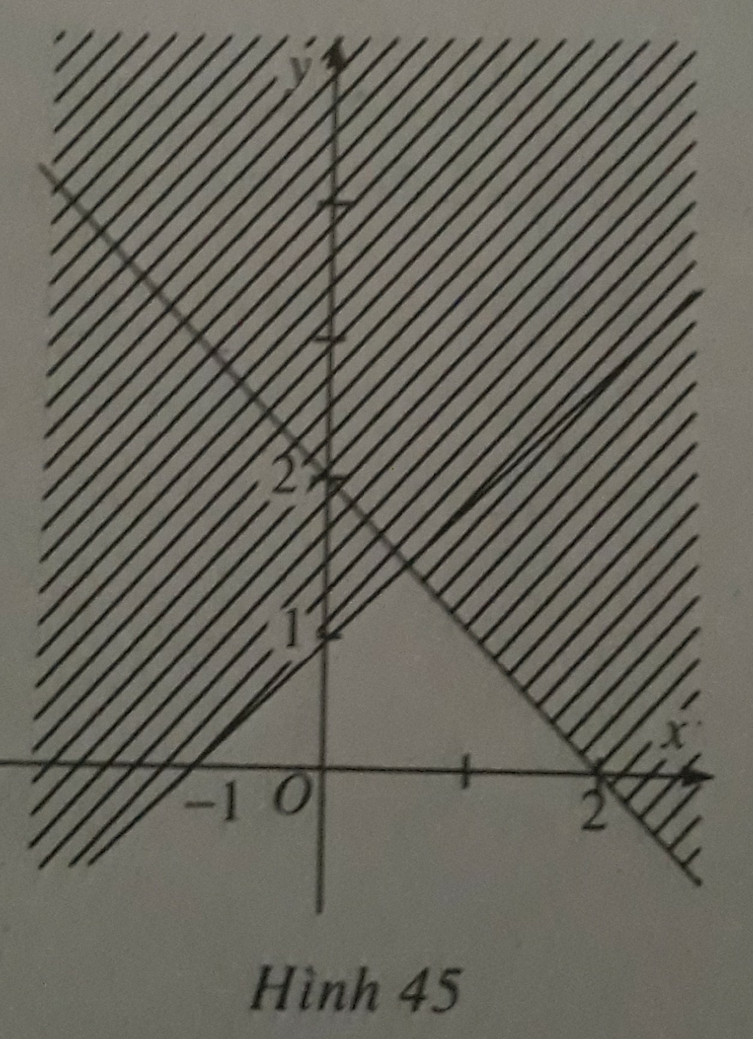
 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
không biết . sorry nha
Khi giải pt và hpt đc phép rút gọn khi biết dấu của biểu thức rút gọn.