Phần 3. Ạ. Cảm ơn nhiều!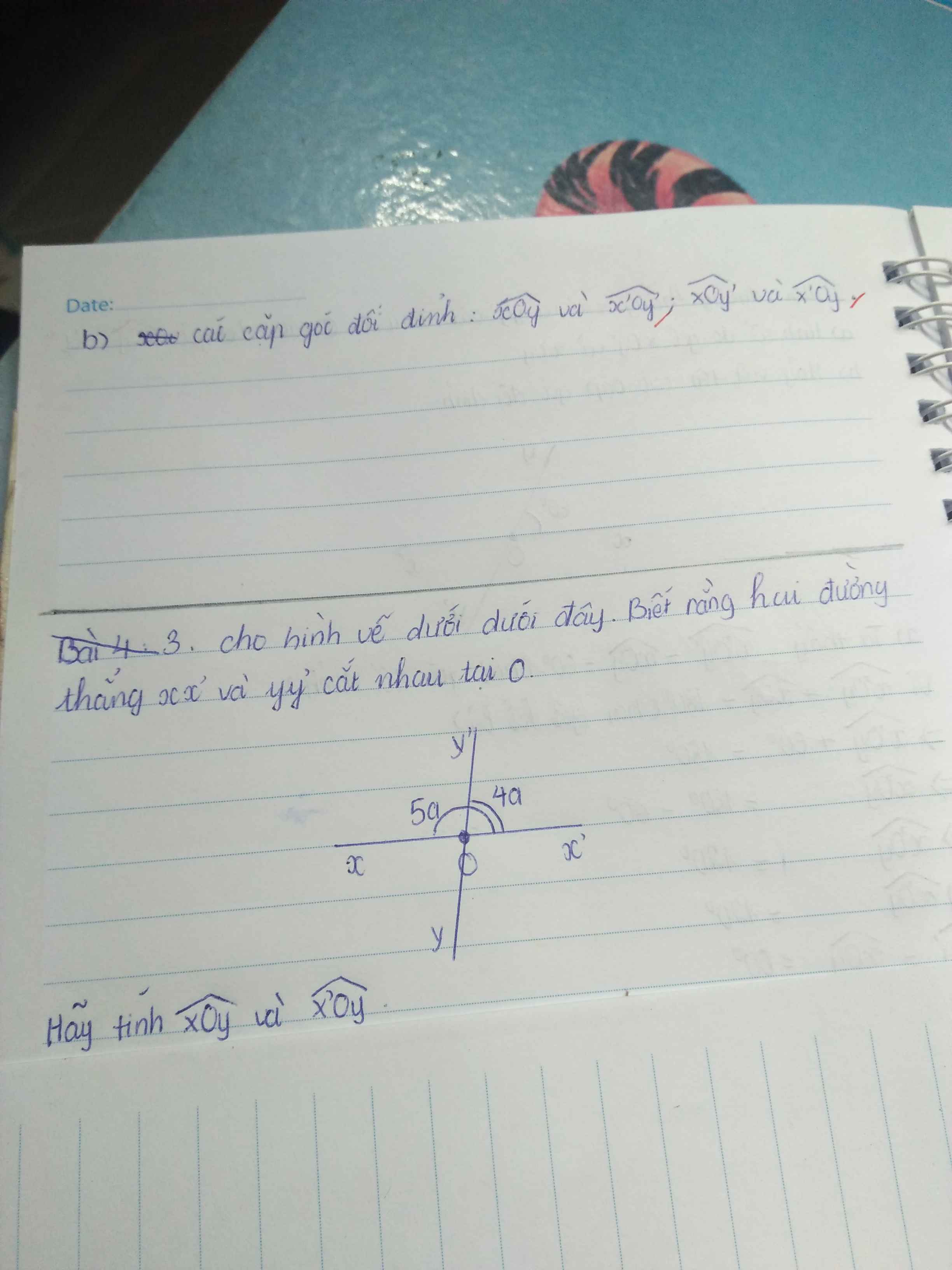 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
1
12 tháng 1 2022
Bài 4:
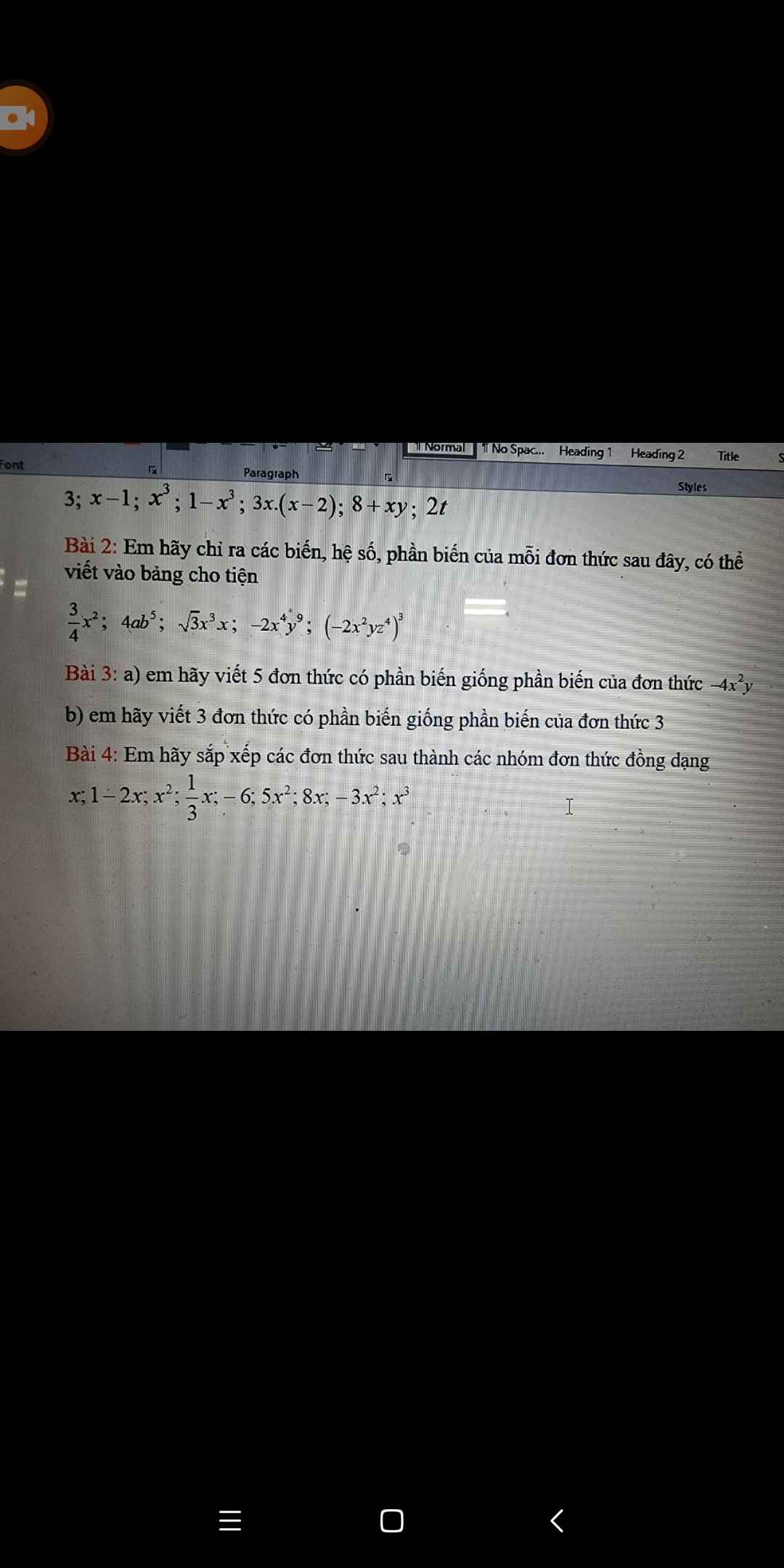
Nhóm 1: x;1/3x; 8x
Nhóm 2: \(x^2;5x^2;-3x^2\)
BD
1
22 tháng 7 2021
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
QN
0
giúp nốt mk phần này với ạ. cảm ơn nhiều
DT
Đỗ Thanh Hải
CTVVIP
5 tháng 4 2021
Lỗi sai
1 C => which
2 C => stopped
3 A => bored
4 B => most
5 B => had stopped
6 C => that
7 C => had knowm
8 A => hadn't been
9 D => learned about
10 B => bỏ
11 B => have come
12 A => would have gone
13 C => would have returned
14 C => knew
15 tháng 1
z4:
\(\dfrac{24}{148}=\dfrac{6}{37}=\dfrac{108}{37\cdot18}\)
\(\dfrac{-14}{-36}=\dfrac{7}{18}=\dfrac{7\cdot37}{18\cdot37}=\dfrac{259}{37\cdot18}\)
mà 108<259
nên \(\dfrac{24}{148}< \dfrac{-14}{-36}\)
z5: \(\dfrac{-26}{-72}=\dfrac{26}{72}< 1\)
\(1< \dfrac{45}{20}=\dfrac{-45}{-20}\)
Do đó: \(\dfrac{-26}{-72}< \dfrac{-45}{-20}\)
z6: \(\dfrac{14}{42}=\dfrac{1}{3}=\dfrac{1\cdot4}{3\cdot4}=\dfrac{4}{12}\)
\(\dfrac{21}{28}=\dfrac{3}{4}=\dfrac{3\cdot3}{4\cdot3}=\dfrac{9}{12}\)
mà 4<9
nên \(\dfrac{14}{42}< \dfrac{21}{28}\)
z7: \(\dfrac{-14}{-56}=\dfrac{1}{4}=\dfrac{5}{20}\)
\(\dfrac{21}{35}=\dfrac{3}{5}=\dfrac{3\cdot4}{5\cdot4}=\dfrac{12}{20}\)
mà 5<12
nên \(\dfrac{-14}{-56}< \dfrac{21}{35}\)
z8: \(10A=\dfrac{10^{201}+10}{10^{201}+1}=1+\dfrac{9}{10^{201}+1}\)
\(10B=\dfrac{10^{202}+10}{10^{202}+1}=1+\dfrac{9}{10^{202}+1}\)
\(10^{201}+1< 10^{202}+1\)
=>\(\dfrac{9}{10^{201}+1}>\dfrac{9}{10^{202}+1}\)
=>\(\dfrac{9}{10^{201}+1}+1>\dfrac{9}{10^{202}+1}+1\)
=>10A>10B
=>A>B
Y
16 tháng 1 2023
\(b,7+3x=3\)
\(\Leftrightarrow3x=-4\)
\(\Leftrightarrow x=-\dfrac{4}{3}\)
\(c,6y+2=20\)
\(\Leftrightarrow6y=18\)
\(\Leftrightarrow y=3\)
\(d,4y=10\)
\(\Leftrightarrow y=\dfrac{10}{4}\)
\(\Leftrightarrow y=\dfrac{5}{2}\)
\(e,5x-7=13\)
\(\Leftrightarrow5x=20\)
\(\Leftrightarrow x=4\)
\(f,\dfrac{4}{3}x+\dfrac{7}{2}=10\)
\(\Leftrightarrow\dfrac{4}{3}x=\dfrac{13}{2}\)
\(\Leftrightarrow x=\dfrac{39}{8}\)
\(g,4-\dfrac{2}{3}y=2\)
\(\Leftrightarrow\dfrac{2}{3}y=2\)
\(\Leftrightarrow y=3\)
\(h,6x=36\Leftrightarrow x=6\)
\(j,7x-3=0\)
\(\Leftrightarrow7x=3\)
\(\Leftrightarrow x=\dfrac{3}{7}\)
ta có: xOy'^+x'Oy'=90o(2 góc kề bù)
⇒5a+4a=90o
⇒9a=90o
⇒a=10o
xOy^=x'Oy'^=4a=4.10o=40o
xOy'^=x'Oy^=5a=5.10o=50o
@ILoveMath Em cảm ơn ạ, đáng ra em phải rep sớm hơn😿