Chất điểm có khối lượng \(m_1=50gam\) dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động \(x_1=\sin(5\pi t+\frac \pi 6)cm\). Chất điểm có khối lượng \(m_2 = 100 gam\) dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động \(x_2=5\sin(\pi t - \frac \pi 6)cm\). Tỉ số cơ năng trong quá trình dao động điều hoà của chất điểm \(m_1\)so với chất điểm \(m_2\)...
Đọc tiếp
Chất điểm có khối lượng \(m_1=50gam\) dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động \(x_1=\sin(5\pi t+\frac \pi 6)cm\). Chất điểm có khối lượng \(m_2 = 100 gam\) dao động điều hoà quanh vị trí cân bằng của nó với phương trình dao động \(x_2=5\sin(\pi t - \frac \pi 6)cm\). Tỉ số cơ năng trong quá trình dao động điều hoà của chất điểm \(m_1\)so với chất điểm \(m_2\) bằng
A.1/2.
B.2.
C.1.
D.1/5.
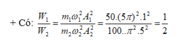
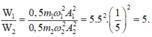
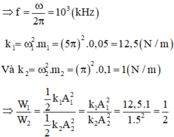
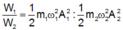
Tỉ số cơ năng
\(\frac{W_1}{W_2}=\frac{k_1A_1^2}{k_2A_2^2}=\frac{m_1\omega_1^2A_1^2}{m_2\omega_2^2A_2^2}=\frac{50.\left(5\pi\right)^21^2}{100.\pi^2.5^2}=\frac{1}{2}\)
Chọn A nhé.