Tìm các điểm có tọa độ nguyên dương trên mặt phẳng thỏa mãn : 2x+5y=200
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
NM
Nguyễn Minh Quang
Giáo viên
2 tháng 1 2022
ta có
\(x^2+y^2-2x+4y=0\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=5\)
Vậy tập hợp các điểm thỏa mãn phương trình trên là đường tròn tâm I( 1,-2) bán kính \(\sqrt{5}\)
PT
1
CM
11 tháng 4 2017
Vế trái là khoảng cách từ điểm biểu diễn z dến điểm biểu diễn z 0 = 0 + i . Vậy tập hợp các điểm thỏa mãn điều kiện đã cho là tất cả các điểm cách điểm (0; 1) một khoảng không đổi bằng 1. Đó là các điểm nằm trên đường tròn bán kính bằng 1 và tâm là điểm (0; 1) (H. 14)
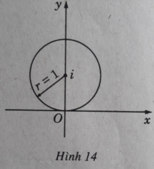
Ta có thể tiến hành như sau:
Cho z = x + iy, ta có | z - 1 | 2 = | x + y - 1 i | 2 = x 2 + y - 1 2 và như vậy ta có: x 2 + y - 1 2 = 1
Đây là phương trình đường tròn bán kính bằng 1 và tâm là (0; 1)
PT
1
CM
28 tháng 8 2018
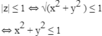
Vậy tập hợp điểm M là hình tròn tâm O(0; 0), bán kính R = 1.
PT
1
CM
16 tháng 12 2019
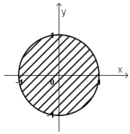
Gọi số phức z = x + y.i có điểm biểu diễn là M(x; y).
|z| = 1 ⇔ x 2 + y 2 = 1 ⇔ x 2 + y 2 =1
Vậy tập hợp điểm M là đường tròn tâm O(0; 0), bán kính R = 1.
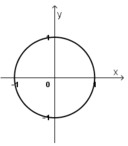
ta có
\(x=\frac{2000-5y}{2}=1000-\frac{5}{2}y\)
vì x, y nguyên dương suy ra 5y chia hết cho 2 suy ra y =2k trong đó \(k\in N\) mà x nguyên dương
suy ra \(0\le1000-\frac{5.2k}{2}\Rightarrow k\le200\)
vậy y=2k với \(k\le200\) và \(x=1000-5k\)