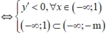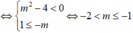tìm tâts cả các số thực m sao cho (CRF) giao với [m-1;m+1) # khác \(\phi\) với F=[1;6)
tìm tất cả các số thực m sao cho tập S không phải con của (E giao F) với S={ x\(\varepsilon R\) / x2 -2(m+1)x +m2 +2m=0 } vỡi E=( \(-\infty\);4), F=[1;6)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 10 2023
\(A=\left[m;m+1\right]\)
\(B=\left[0;3\right]\)
\(A\cap B=\varnothing\)
\(\Leftrightarrow\left[{}\begin{matrix}m+1< 0\\m>3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>3\end{matrix}\right.\) thỏa mãn đề bài
CM
8 tháng 4 2019
Đáp án B
Điều kiện để hai đồ thị hàm số đã cho tiếp xúc nhau là
f x = g x f ' x = g ' x có ít nhất một nghiệm.
⇔ x 3 − m x + 1 = x 2 + 1 3 x 2 − m = 2 x ⇔ x 3 − m x = x 2 3 x 3 − m x = 2 x 2 ⇔ 2 x 3 = x 2 3 x 2 − 2 x = m
⇔ x 2 2 x − 1 = 0 m = 3 x 2 − 2 x ⇔ x = 0 x = 1 2 m = 3 x 2 − 2 x ⇔ m = 0 m = − 1 4 .
Vậy m = 0 hoặc m = − 1 4 .
CM
6 tháng 9 2017
Chọn đáp án D
.
Ta có y ' = m 2 - 4 x + m 2 .
Hàm số luôn đơn điệu trên từng khoảng - ∞ ; - m và - m ; + ∞ .
Hàm số giảm trên khoảng - ∞ ; 1 tức là hàm số nghịch biến trên khoảng - ∞ ; 1 .
