LẬP CHƯƠNG TRÌNH GIẢI PHƯƠNG TRÌNH BẬC HAI
AX^2+BC+C=0
(GIẢ THIẾT DELTA KO ÂM )
AI TRẢ LỜI ĐÚNG VÀ NHANH MK CHO 3 ****
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
Thuật toán:
B1: Nhập a,b,c
B2: Tính \(\Delta\) = b2-4ac;
B3: Kiểm tra nếu \(\Delta\) >0 phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{-b+\sqrt{\Delta}\text{ }}{2a}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}\)
B4: Kiểm tra nếu \(\Delta\)<0 thì phương trình vô nghiệm
B5: Kiểm tra nếu \(\Delta\)=0 phương trình có 2 nghiệm kép \(x_1=x_2=-\dfrac{b}{2a}\)
Viết chương trình:
Program HOC24;
var a,b,c: integer;
x1,x2: real;
denta: longint;
begin
write('Nhap a; b; c: '); readln(a,b,c);
denta:=b*b-4*a*c;
if denta>0 then
begin
write('x1= ',(-b+sqrt(denta))/(2*a):1:2);
write('x2= ',(-b-sqrt(denta))/(2*a):1:2);
end;
if denta<0 then write('Phuong trinh vo nghiem');
if denta=0 then write('x= ',-b/2*a:1:2);
readln
end.
Bài 2:
Thuật toán:
B1: Nhập a,b
B2: Kiểm tra nếu a=0 và b=0 thì phương trình có vô số nghiệm
B3: Kiểm tra nếu a=0 thì phương trình vô nghiệm
B4: Kiểm tra nếu a khác 0 thì có nghiệm x=-b/a;
Viết chương trình:
Program HOC24;
var a,b: integer;
x: real;
begin
write('Nhap a; b: '); readln(a,b);
if a=0 and b=0 then write('Phuong trinh co vo so nghiem');
if a=0 then write('Phuong trinh vo nghiem');
if a<>0 then write('x=',-b/a:1:2);
readln
end.

Đáp án: A
Bước 1 sai vì giả sử phản chứng sai, phải giả sử phương trình vô nghiệm và a, c trái dấu.

const fi='dulieu.inp';
fo='kq.inp';
var f1,f2:text;
a,b,c,delta:real;
begin
assign(f1,fi); reset(f1);
assign(f2,fo); rewrite(f2);
readln(f1,a,b,c);
delta:=sqr(b)-4*a*c;
if delta<0 then writeln(f2,'Phuong trinh vo nghiem');
if delta=0 then writeln(f2,'Phuong trinh co nghiem kep la: ',-b/(2*a):4:2);
if delta>0 then
begin
writeln(f2,'Nghiem thu nhat la: ',(-b+sqrt(delta))/(2*a):4:2);
writeln(f2,'Nghiem thu hai la: ',(-b-sqrt(delta))/(2*a):4:2);
end;
close(f1);
close(f2);
end.

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
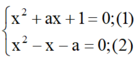
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.

Nghiệm chung x (nếu có) của hai phương trình là nghiệm của hệ:
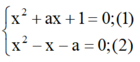
Lấy (1) trừ (2) vế trừ vế ta được:
ax + 1+ x+ a = 0
⇔ ( ax+ x) + (1+ a) =0
⇔ (a+ 1).x+ (1+ a) = 0
⇔ ( a+ 1) . (x+1)=0
⇔ a = - 1 hoặc x= -1
* Với a = -1 thay vào (2) ta được: x 2 - x + 1 = 0 phương trình này vô nghiệm
vì ∆ = ( - 1 ) 2 – 4 . 1 . 1 = - 3 < 0
nên loại a = -1.
*Thay x = -1 vào (2) suy ra a = 2.
Vậy với a = 2 thì phương trình có nghiệm chung là x = -1
Vậy chọn câu C.

Đáp án: D
Theo định lý Vi-ét ta có
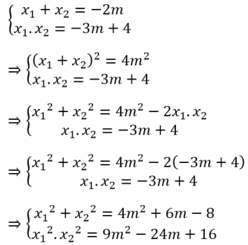
Khi đó, ![]() là nghiệm của phương trình
là nghiệm của phương trình
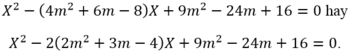

gọi số tuổi của Phương năm nay là x thì số tuổi của mẹ Phương năm nay là 3x
sau 13 năm nữa: thì số tuổi của Phương là X+13
: còn số tuổi của mẹ Phương là 3x+13
mà lúc nay số tuổi của mẹ chỉ gấp 2 lần Phương nên ta có pt
3x+13=2(X+13)
3x+13=2x+26
x=13

Bài làm
\(ax^2+bx+c=0\)
Theo định lý Viet :
\(\hept{\begin{cases}x_1+x_2=\frac{-b}{a}\\x_1\cdot x_2=\frac{c}{a}\end{cases}}\)
Ta có:\(\hept{\begin{cases}\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=5\left(x_1+x_2\right)\\\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=6x_1^2+4x,x_2+6x^2_2+9x,x_2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=\frac{-5b}{a}\\\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=6\left(x_1+x_2\right)^2+x_1\cdot x_2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=\frac{-5b}{a}\\\left(2x_1+3x_2\right)+\left(3x_1+2x_2\right)=\frac{+6b^2}{a^2}+\frac{c}{a}\end{cases}}\)
Vậy \(\left(2x_1+3x_2\right)\)và \(\left(3x_1+2x_2\right)\)là n của pt:
\(X^2-\left(\frac{-5b}{a}\right)X+\frac{6b^2}{a^2}+\frac{c}{a}=0\)
\(X^2+\frac{5b}{a}X+\frac{6b^2}{a^2}+\frac{c}{a}=0\)
~Hok tốt nhé~