Ví dụ 1: Số giá trị nguyên của tham số m để hàm số 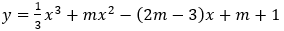không có cực trị...
Đọc tiếp
Ví dụ 1: Số giá trị nguyên của tham số m để hàm số 
không có cực trị là:
A. 5
B. 1
C. 4
D. 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NP
1
Những câu hỏi liên quan
CM
5 tháng 10 2017
Chọn D.
⇒ Hàm số đạt cực tiểu tại x = 0
⇒ Khi m = 0 hàm số không có cực đại
⇒ m = 0 thỏa mãn
Ta có
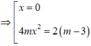
Để hàm số y = m x 4 - m - 3 x 2 + m 2 không có điểm cực đại
+) (*) vô nghiệm
⇒ Hàm số chỉ có 1 cực trị x = 0
Để x = 0 là điểm cực tiểu
⇔ m < 3
⇒ 0 < m < 3
+) (*) có nghiệm kép x = 0 ⇒ m = 3
Khi đó y ' = 12 x 3 = 0 ⇔ x = 0
Qua điểm x = 0 ta thấy y ' đổi dấu từ âm sang dương
⇒ x = 0 là điểm cực tiểu
⇒ m = 3 thỏa mãn.
+) (*) có 2 nghiệm phân biệt
⇒ Hàm số luôn có cực đại ⇒ Loại.
Vậy để hàm số đã cho không có cực đại thì 0 ≤ m ≤ 3
Mà m ∈ Z ⇒ m ∈ 0 ; 1 ; 2 ; 3
CM
1 tháng 10 2019
Chọn B.
Phương pháp: v
Cách giải: Ta có
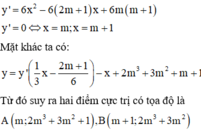
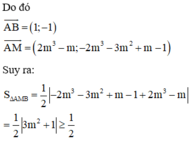
Dấu bằng xảy ra khi m = 0.
Vậy có duy nhất một giá trị của m thỏa mãn yêu cầu bài toán.
CM
20 tháng 6 2019
Đáp án D.
Ta có f ' x = 6 x 2 - 12 x ; f ' x = 0 ⇔ [ x = 0 ⇒ y 0 = 1 - m x = 2 ⇒ y 2 = - 7 - m .
Theo bài ra, ta có y 0 . y 2 < 0 ⇔ 1 - m - 7 - m < 0 ⇔ - 7 < m < 1 .
CM
5 tháng 11 2019
Đáp án B
Ta có y ' = 4 x 3 - 4 m 2 + 1 x , ∀ x ∈ ℝ . Phương trình y ' = 0 ⇔ [ x = 0 x = m 2 + 1 .
Hệ số a > 0 suy ra giá trị cực tiểu của hàm số là y C T = 2 - m 2 + 1 4 ≤ 1
Dấu “=” xảy ra khi và chỉ khi m 2 = 0 ⇒ m = 0 .
\(D=ℝ\)
\(y=\frac{1}{3}x^3+mx^2-\left(2m-3\right)x+m+1\)
\(y'=x^2+2mx-\left(2m-3\right)\)
Để hàm số không có cực trị thì phương trình \(y'=0\)vô nghiệm hoặc có nghiệm kép.
\(\Delta'=m^2+2m-3,\Delta'\le0\Leftrightarrow-3\le x\le1\)
Có các giá trị \(x\)nguyên là \(-3,-2,-1,0,1\).
Tổng cộng có \(5\)giá trị.
Chọn A.