Tìm năm số khác nhau trong dãy tính sau đây: ( * * + ** + ** ) : ** = **
Biết rằng :
Ba số hạng trong dấu ngoặc thì một số hạng là BCNN của hai số hạng kia.
Số chia là số nguyên tố và là UCLN của hai số nói trên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
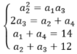
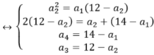
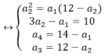
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D
Đặt số chia là p (p là số nguyên tố, \(11\le p< 100\)). Suy ra ba số hạng trong ngoặc sẽ là pmn, pm, pn, với (m,n)=1.
Mặt khác, do các số phải tìm là khác nhau nên \(mn\ge6.\)Từ đó, ta có:
\(p< \frac{100}{6}< 17\Rightarrow p=1;13\)
Ta có, thương của phép tính đã cho luôn là m + n + mn, do vậy xét hai trường hợp:
Trường hợp 1: Với p = 11, ta có:
\(6\le mn< 10\Rightarrow mn=6\Rightarrow m+n+mn=11\)
Không thỏa mãn do \(p\ne m+n+mn.\)
Trường hợp 2:Với p = 13, ta có:
\(6\le mn< 8\Rightarrow mn=6\Rightarrow m+n+mn=11\)
Vậy năm số phải tìm là 78,39,26,13,11.
Ta được dãy tính như sau (73 + 39 + 26):13 = 11