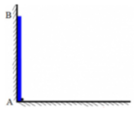
hình bên minh họa một miếng ván dựa vào bức tường thẳng đứng và trượt trên tường từ vị trí AB đến vị trí CD. biết OC = 4 AC, BD = 2 AC và OB = 5 cm Tìm chiều dài của miếng ván
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

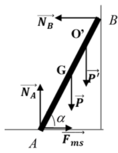
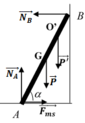
a. Trọng lượng của thanh: P = mg = 200N
Theo điều kiện cân bằng Momen
M P → = M N → B ⇒ P . A B 2 cos α = N B . A B . sin α
Theo điều kiện cân bằng lực
P → + N → A + N → B + F → m s = 0 → N A = P = 200 N ; F m s = N B ⇒ N B = F m s = P 2 = 100 N
b, Điều kiện: Fms <k.NA
Theo câu a F m s = N B = P 2 t g α
⇒ N A = P ⇒ t g α > 1 2 k = 1 1 , 2 ⇒ α = 40 0
c. Lấy O’ là vị trí người khi thang bắt đầu trượt.
Ta có:
N B = F m s = k N A ; N A = P + P ' = 600 N F m s = 360 N
Xét trục quay qua A
M N → B = M P → + M P ' → N B . A B sin α = P . A B 2 . cos α + P ' . A O ' . cos α ⇒ A O ' = 1 , 3 m


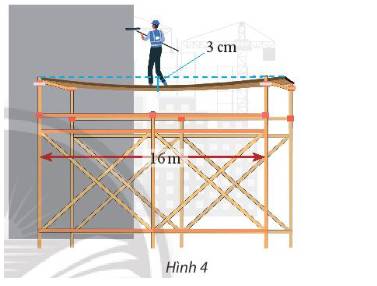
a) Ta vẽ lại parabol và chọn hệ trục tọa độ như hình dưới
Giả sử phương trình chính tắc của parabol có dạng \({y^2} = 2px\)
Từ giả thiết ta có: \(AB = 2{y_A} = 16 \Rightarrow {y_A} = 8 \Rightarrow A\left( {0,03;8} \right)\)
Thay tọa độ điểm A vào phương trình \({y^2} = 2px\)ta được \({8^2} = 2p.0,03 \Rightarrow p = \frac{{3200}}{3}\)
Vậy Phương trình chính tắc của parabol có dạng \({y^2} = \frac{{6400}}{3}x\)
b) Thay \(x = 1\)vào phương trình \({y^2} = \frac{{6400}}{3}x\) ta có \({y^2} = \frac{{6400}}{3}.1 \Rightarrow y = \frac{{80\sqrt 3 }}{3} \simeq 46,2\)
Vậy điểm có độ võng 1 cm cách tâm ván gỗ gần bằng 46,2 m
Chú ý khi giải: đổi về cùng đơn vị đo

Chọn D.
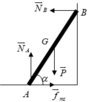
Lấy O’ là vị trí người khi thang bắt đầu trượt.
Theo điều kiện cân bằng lực:
![]()
→NB = Fms = k.NA; NA = P + P’ = 600 N
Fms = 360N
Xét trục quay qua A: