Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(\sqrt[]{3x+7}-5< 0\)
\(\Leftrightarrow\sqrt[]{3x+7}< 5\)
\(\Leftrightarrow3x+7\ge0\cap3x+7< 25\)
\(\Leftrightarrow x\ge-\dfrac{7}{3}\cap x< 6\)
\(\Leftrightarrow-\dfrac{7}{3}\le x< 6\)

\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
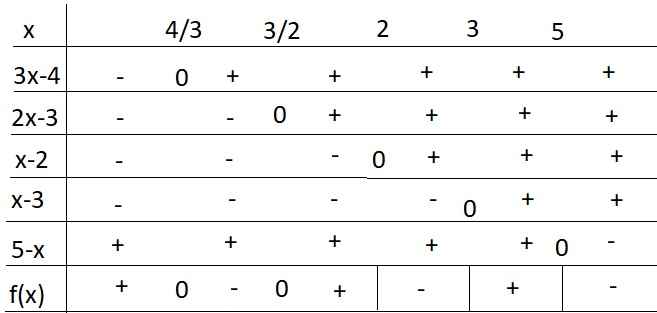
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)

1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4

Chọn C
ĐKXĐ:
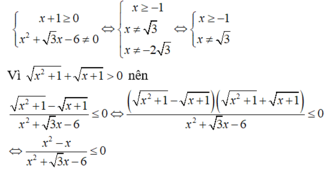
Bảng xét dấu
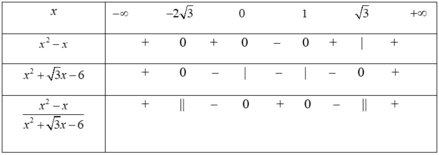
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là
![]()

a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4
d: =>3x>=9
=>x>=3

Lời giải:
b/
\(\frac{3x+5}{2x^2-5x+3}\geq 0\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} 3x+5\geq 0\\ 2x^2-5x+3>0\end{matrix}\right.\\ \left\{\begin{matrix} 3x+5\leq 0\\ 2x^2-5x+3<0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow \left[\begin{matrix} \left\{\begin{matrix} x\geq \frac{-5}{3}\\ x>\frac{3}{2}(\text{hoặc}) x< 1\end{matrix}\right.\\ \left\{\begin{matrix} x\leq \frac{-5}{3}\\ 1< x< \frac{3}{2}\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow \left[\begin{matrix} x>\frac{3}{2}\\ \frac{-5}{3}\leq x< 1\end{matrix}\right.\ \)
c/
$2x^3+x+3>0$
$\Leftrightarrow 2x^2(x+1)-2x(x+1)+3(x+1)>0$
$\Leftrightarrow (x+1)(2x^2-2x+3)>0$
$\Leftrightarrow (x+1)[x^2+(x-1)^2+2]>0$
$\Leftrightarrow x+1>0$
$\Leftrightarrow x>-1$

`|5x| = - 3x + 2`
Nếu `5x>=0<=> x>=0` thì phương trình trên trở thành :
`5x =-3x+2`
`<=> 5x +3x=2`
`<=> 8x=2`
`<=> x= 2/8=1/4` ( thỏa mãn )
Nếu `5x<0<=>x<0` thì phương trình trên trở thành :
`-5x = -3x+2`
`<=>-5x+3x=2`
`<=> 2x=2`
`<=>x=1` ( không thỏa mãn )
Vậy pt đã cho có nghiệm `x=1/4`
__
`6x-2<5x+3`
`<=> 6x-5x<3+2`
`<=>x<5`
Vậy bpt đã cho có tập nghiệm `x<5`

A, 3X+6>0
(=)3X>-6
 (=)X>-2
(=)X>-2
VẬY ...
B,10-2X≥-4
![]() (=)-2X≥-4-10
(=)-2X≥-4-10
 (=)-2X≥-14
(=)-2X≥-14
(=)X≤7
VẬY....
C, ![]()
![]() (=)
(=)![]()
(=) -15X+10>-3+3X
 (=)-15X-3X>-3-10
(=)-15X-3X>-3-10
(=)-18X>-13
(=)X<![]()
Trả lời:
\(\left(-3x+6\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\hept{\begin{cases}-3x+6< 0\\x-5>0\end{cases}}\) hoặc \(\hept{\begin{cases}-3x+6>0\\x-5< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>2\\x>5\end{cases}}\) hoặc \(\hept{\begin{cases}x< 2\\x< 5\end{cases}}\)
Vậy x > 5; x < 2 là nghiệm của pt.
\(\left(-3x+6\right)\left(x-5\right)< 0\)
\(\Leftrightarrow-3\left(x-2\right)\left(x-5\right)< 0\)
\(\Leftrightarrow\left(x-2\right)\left(x-5\right)>0\)
\(\Leftrightarrow\hept{\begin{cases}x-2>0\\x-5>0\end{cases}}\)hoặc \(\hept{\begin{cases}x-2< 0\\x-5< 0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x>2\\x>5\end{cases}}\)hoặc \(\hept{\begin{cases}x< 2\\x< 5\end{cases}}\)
hay \(\orbr{\begin{cases}x>5\\x< 2\end{cases}}\)
Vậy nghiệm của BPT là \(x>5\)hoặc \(x< 2\)