 Giúp mình bài 7;10;11 ạ
Giúp mình bài 7;10;11 ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Bài 6:
a: \(\sqrt{\dfrac{2}{3-\sqrt{5}}}=\dfrac{\sqrt[4]{2}\cdot\left(\sqrt[2]{5}+1\right)}{2}\)
b: \(\sqrt{\dfrac{a-4}{2\left(\sqrt{a}-2\right)}}=\dfrac{\sqrt{2}\left(\sqrt{a}+2\right)}{2}\)

Bài 7:
a: ĐKXĐ: \(x\notin\left\{\dfrac{1}{2};-5\right\}\)
\(\dfrac{x+5}{2x-1}-\dfrac{1-2x}{x+5}-2=0\)
=>\(\dfrac{x+5}{2x-1}+\dfrac{2x-1}{x+5}-2=0\)
=>\(\dfrac{\left(x+5\right)^2+\left(2x-1\right)^2}{\left(2x-1\right)\left(x+5\right)}=2\)
=>\(\left(x+5\right)^2+\left(2x-1\right)^2=2\left(2x-1\right)\left(x+5\right)\)
=>\(x^2+10x+25+4x^2-4x+1=2\left(2x^2+10x-x-5\right)\)
=>\(5x^2+6x+26-4x^2-18x+10=0\)
=>\(x^2-12x+36=0\)
=>\(\left(x-6\right)^2=0\)
=>x-6=0
=>x=6(nhận)
b: ĐKXĐ: \(x\notin\left\{3;-2;4\right\}\)
\(1-\dfrac{8}{x-4}=\dfrac{5}{3-x}-\dfrac{8-x}{x+2}\)
=>\(\dfrac{x-4-8}{x-4}=\dfrac{-5}{x-3}+\dfrac{x-8}{x+2}\)
=>\(\dfrac{x-12}{x-4}=\dfrac{-5\left(x+2\right)+\left(x-8\right)\left(x-3\right)}{\left(x-3\right)\left(x+2\right)}\)
=>\(\dfrac{x-12}{x-4}=\dfrac{-5x-10+x^2-11x+24}{\left(x-3\right)\left(x+2\right)}\)
=>\(\left(x-12\right)\left(x^2-x-6\right)=\left(x-4\right)\left(x^2-16x+14\right)\)
=>\(x^3-x^2-6x-12x^2+12x+72=x^3-16x^2+14x-4x^2+64x-56\)
=>\(-13x^2+6x+72=-20x^2+78x-56\)
=>\(7x^2-72x+128=0\)
=>\(\left[{}\begin{matrix}x=8\left(nhận\right)\\x=\dfrac{16}{7}\left(nhận\right)\end{matrix}\right.\)
c: ĐKXĐ: \(x\notin\left\{2;-2\right\}\)
\(\dfrac{x-1}{x+2}+\dfrac{2}{x-2}=\dfrac{12}{x^2-4}\)
=>\(\dfrac{x-1}{x+2}+\dfrac{2}{x-2}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}\)
=>\(\dfrac{\left(x-1\right)\left(x-2\right)+2\left(x+2\right)}{\left(x+2\right)\left(x-2\right)}=\dfrac{12}{\left(x-2\right)\left(x+2\right)}\)
=>\(x^2-3x+2+2x+4=12\)
=>\(x^2-x-6=0\)
=>(x-3)(x+2)=0
=>\(\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)

\(7,\\ a,=\left(3x+1\right)^3\\ b,=\left(2x+3y\right)^3\\ c,mờ.quá\\ d,=\left(3x-1\right)^3\\ e,=\left(\dfrac{x}{2}+y^2\right)^3\\ 8,\\ a,=\left(x+3\right)^3\\ b,=\left(2-x\right)^3\)

Bài 7:
\(\widehat{AOB}+\widehat{A}+\widehat{B}=360^0\)
nên Ax//By

Câu 7 :
a, Tham khảo : https://olm.vn/hoi-dap/detail/43902845942.html
b, Tham khảo : https://olm.vn/hoi-dap/detail/7963533510.html








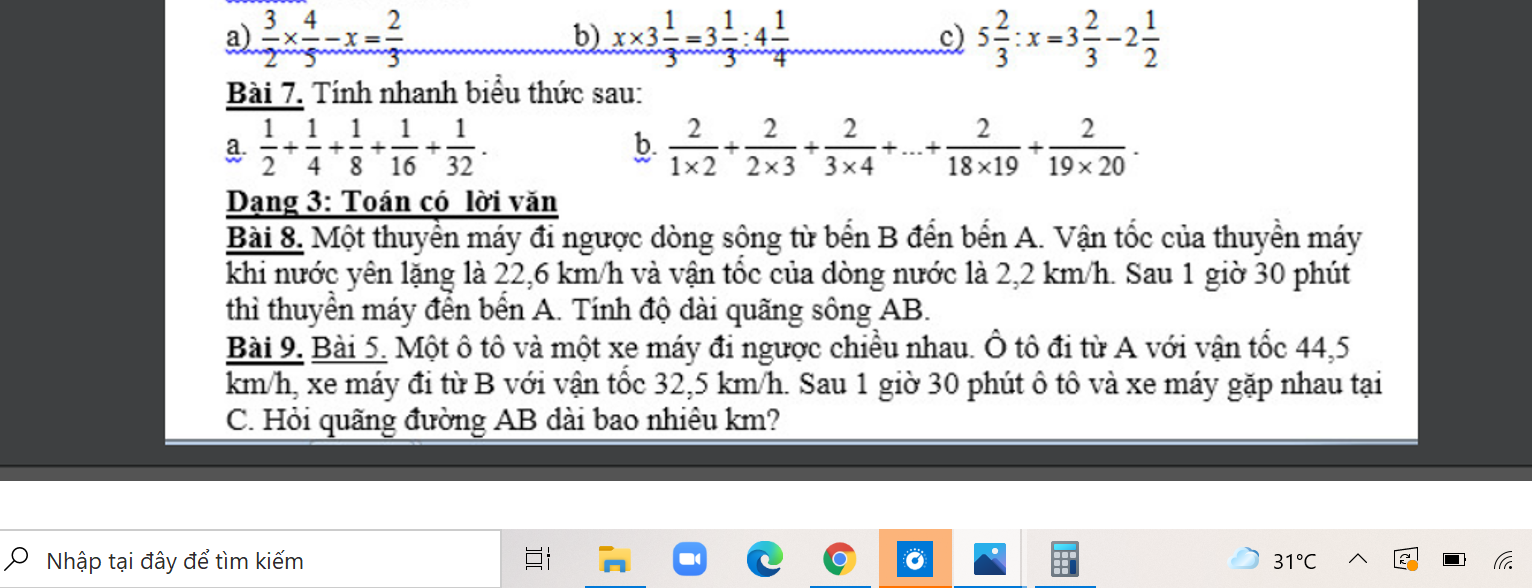 các bạn giúp mình bài 7, bài 8, bài 9 nhé. cần gấp ạ
các bạn giúp mình bài 7, bài 8, bài 9 nhé. cần gấp ạ
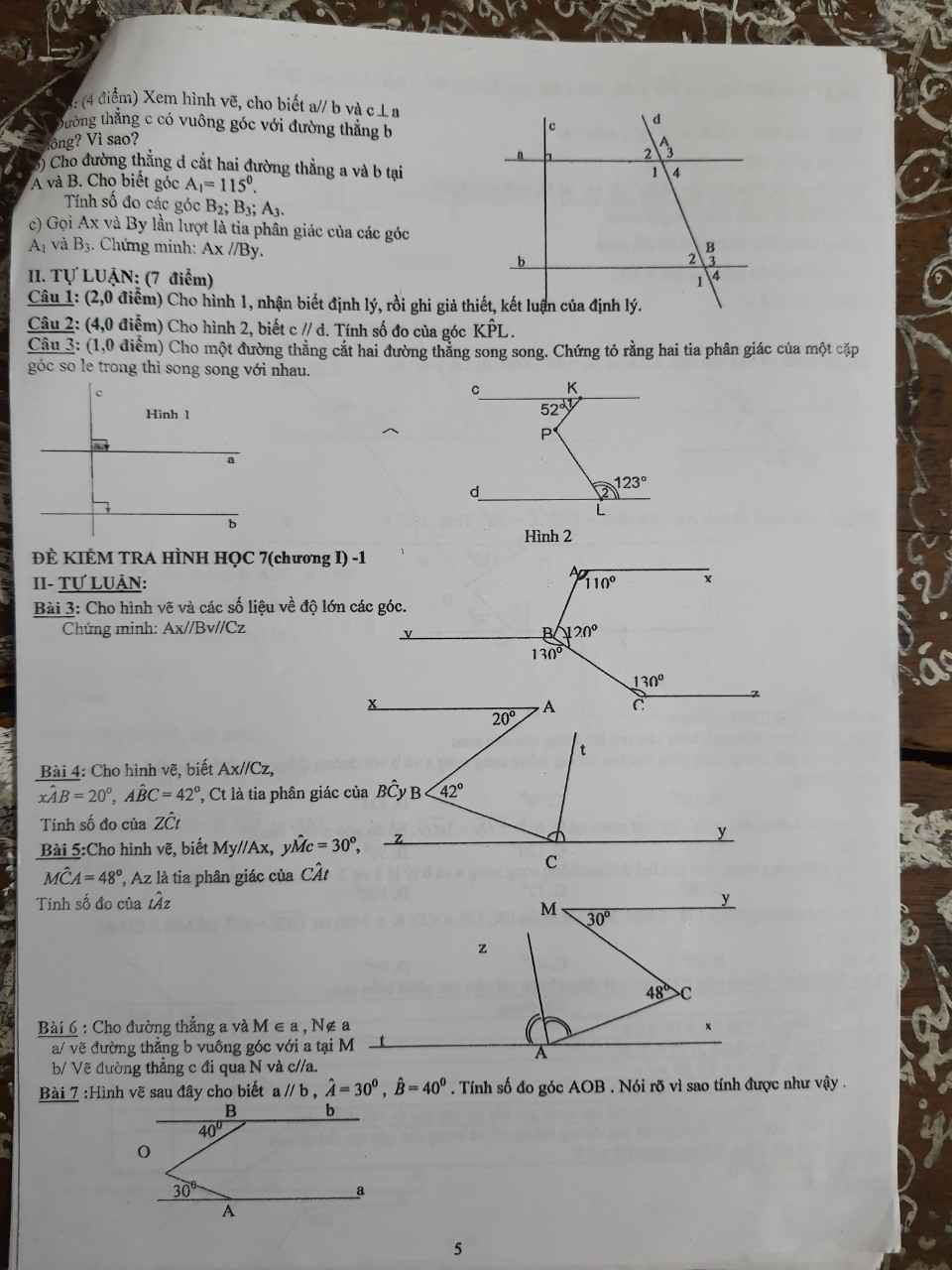
Bài 7.
a) \(\sqrt{x+9}=3\)(ĐK: \(x\ge-9\))
\(\Leftrightarrow x+9=3^2\)
\(\Leftrightarrow x=0\)(thỏa mãn)
b) \(\sqrt{2x^2+2}=3x-1\)
\(\Rightarrow2x^2+2=\left(3x-1\right)^2\)
\(\Leftrightarrow7x^2-6x-1=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=1\\x=-\frac{1}{7}\end{cases}}\)
Thử lại chỉ có \(x=1\)thỏa mãn.
c) \(\sqrt{x^2-2x+1}=19x-1\)
\(\Rightarrow x^2-2x+1=\left(19x-1\right)^2\)
\(\Leftrightarrow360x^2-36x=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{1}{10}\end{cases}}\)
Thử lại chỉ có \(x=\frac{1}{10}\)thỏa mãn.
d) \(\sqrt{x^2-x-6}=\sqrt{x-3}\)(ĐK: \(x\ge3\))
\(\Rightarrow x^2-x-6=x-3\)
\(\Leftrightarrow x^2-2x-3=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-1\left(l\right)\\x=3\left(tm\right)\end{cases}}\)
e) \(\sqrt{4x^2+4x+1}=\sqrt{x^2+12x+36}\)
\(\Leftrightarrow\left|2x+1\right|=\left|x+6\right|\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=x+6\\2x+1=-x-6\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=5\\x=-\frac{7}{3}\end{cases}}\)
g) \(\sqrt{x+4\sqrt{x-4}}=2\)(ĐK: \(x\ge4\))
\(\Leftrightarrow\sqrt{x-4+4\sqrt{x-4}+4}=2\)
\(\Leftrightarrow\left|\sqrt{x-4}-2\right|=2\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{x-4}-2=2\\\sqrt{x-4}-2=-2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=20\\x=4\end{cases}}\)(thỏa mãn)
Bài 10.
b) \(\sqrt{x^2-2x+4}=x-1\)
\(\Rightarrow x^2-2x+4=\left(x-1\right)^2\)
\(\Leftrightarrow0x=3\)(vô nghiệm)
c) \(\sqrt{x^2-6x+9}=4-x\)
\(\Leftrightarrow\left|x-3\right|=4-x\)
\(\Rightarrow\orbr{\begin{cases}x-3=4-x\\x-3=x-4\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}2x=7\\0x=1\end{cases}}\)
\(\Leftrightarrow x=\frac{7}{2}\)(thử lại thỏa mãn)
d) \(\sqrt{x^2-2x+1}+\sqrt{x^2-4x+4}=3\)
\(\Leftrightarrow\left|x-1\right|+\left|x-2\right|=3\)
Với \(x\ge2\):
\(x-1+x-2=3\)
\(\Leftrightarrow x=3\)(thỏa mãn)
Với \(1\le x< 2\):
\(x-1+2-x=3\)
\(\Leftrightarrow0x=2\)(vô nghiệm)
Với \(x< 1\):
\(1-x+2-x=3\)
\(\Leftrightarrow x=0\)(thỏa mãn)