ai giải dùm e với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
8
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
2.2 Đề lỗi không dịch được
2.3
\(\Delta'=4m^2-2\left(2m^2-1\right)=2>0\Rightarrow\) pt luôn có 2 nghiệm pb
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=\dfrac{2m^2-1}{2}\end{matrix}\right.\)
\(\Rightarrow\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=2\Rightarrow\left[{}\begin{matrix}x_1-x_2=\sqrt{2}\\x_1-x_2=-\sqrt{2}\end{matrix}\right.\)
Do \(x_1\) là nghiệm của pt nên ta có:
\(2x_1^2-4mx_1+2m^2-1=0\Rightarrow2x_1^2=4mx_1-2m^2+1\)
Thế vào bài toán:
\(4mx_1-2m^2+1-4mx_2+2m^2-9< 0\)
\(\Leftrightarrow m\left(x_1-x_2\right)< 2\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{2}m< 2\\-\sqrt{2}m< 2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m< \sqrt{2}\\m>-\sqrt{2}\end{matrix}\right.\)
(Bản thân câu này đề bài cũng rất dở)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
Áp dụng BĐT Cô-si:
\(\dfrac{x^2}{x+1}+\dfrac{x+1}{9}\ge2\sqrt{\dfrac{x^2\left(x+1\right)}{9\left(x+1\right)}}=\dfrac{2}{3}x\)
\(\dfrac{y^2}{y+1}+\dfrac{y+1}{9}\ge2\sqrt{\dfrac{y^2\left(y+1\right)}{9\left(y+1\right)}}=\dfrac{2}{3}y\)
Cộng vế:
\(\dfrac{x^2}{x+1}+\dfrac{y^2}{y+1}+\dfrac{x+y+2}{9}\ge\dfrac{2}{3}\left(x+y\right)\)
\(\Leftrightarrow P+\dfrac{1+2}{9}\ge\dfrac{2}{3}.1\)
\(\Rightarrow P\ge\dfrac{1}{3}\)
\(P_{min}=\dfrac{1}{3}\) khi \(x=y=\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 1
Áp dụng BĐT Cô-si:
\(3\left(a^2+4\right)\ge3.4a=12a\)
\(b^4+b^4+b^4+81\ge4\sqrt[4]{81b^{12}}=12b^3\)
Cộng vế:
\(3\left(a^2+b^4\right)+93\ge12\left(a+b^3\right)=384\)
\(\Rightarrow a^2+b^4\ge85\)
\(\Rightarrow P\ge85-19=66\)
\(P_{min}=66\) khi \(\left(a;b\right)=\left(2;3\right)\)
DT
1
29 tháng 12 2021
Câu 5:
\(\Leftrightarrow-x^2+7x-9+2x-9=0\)
\(\Leftrightarrow x^2-9x+18=0\)
=>x=3
=>Chọn A
AH
Akai Haruma
Giáo viên
20 tháng 2 2022
Lời giải:
$\Delta'=(m-1)^2-(m+1)=m^2-3m=m(m-3)$
Áp dụng định lý Viet, với $x_1,x_2$ là 2 nghiệm của pt thì:
$x_1+x_2=2(m-1)$
$x_1x_2=m+1$
a. Để pt có 2 nghiệm trái dấu thì \(\left\{\begin{matrix} \Delta '>0\\ x_1x_2<0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m(m-3)>0\\ m+1<0\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} m>3 \text{or} m< 0\\ m< -1\end{matrix}\right.\Leftrightarrow m< -1\)
b. Có 2 nghiệm pb khi mà $\Delta'=m(m-3)>0$
$\Leftrightarrow m>3$ hoặc $m< 0$
c.
Có 2 nghiệm dương pb khi mà \(\left\{\begin{matrix} \Delta'>0\\ x_1+x_2>0\\ x_1x_2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m(m-3)>0\\ 2(m-1)>0\\ m+1>0\end{matrix}\right.\Leftrightarrow m>3\)
d.
PT có 1 nghiệm dương khi mà:
TH1: Nó có 2 nghiệm trái dấu (kết quả giống phần a)
TH2: Nó có 1 nghiệm kép dương. Có nghiệm kép khi mà $\Delta'=0\Leftrightarrow m=0$ hoặc $m=3$
Thay lần lượt 2 giá trị này vô pt ban đầu suy ra $m=3$
TH3: Nó có 1 nghiệm dương 1 nghiệm =0
PT có nghiệm $=0\Leftrightarrow 0^2-2(m-1).0+m+1=0$
$\Leftrightarrow m=-1$
Thay trở lại pt ban đầu thì nghiệm còn lại $=-4<0$ (loại)
Vậy...........
21 tháng 2 2022
Khổ thơ thứ 2 ,3đã diễn tả những cảm nhân tinh tế của nhà thơ về những biến chuyển của đất trời trong khoảnh khắc giao mùa. Đến đây, nhà thơ không còn những mơ hồ, hoài nghi về khí thu se lạnh đã chạm ngõ. Thiên nhiên sang thu đã được cụ thể bằng những hình ảnh: “sông dềnh dàng”, “chim vội vã”, “đám mây vắt nửa mình”. Bằng phép nhân hóa đặc sắc, nhà thơ đã rất tài hoa ghi lại linh hồn của cảnh vật, của dòng sông quê hương nơi vùng đồng bằng Bắc Bộ ăm ắp nước phù sa. Cái dềnh dàng của sông là sau lúc vượt thác leo ghềnh nhọc nhằn , đã đến lúc được nghỉ ngơi sau bao mùa mưa lũ. Còn bầy chim, khi mùa thu chợt đến, nó phải gấp gáp để làm tôt tha mồi. Câu thơ cho thấy 2 tốc độ trái chiều giữa dòng sông và cánh chim, cũng là quy luật không đồng đều ở vào thời điểm giao thoa của muôn vật muôn loài. Sự chuyển mình sang thu không chỉ được biểu hiện qua sự đối lập trong hoạt động của con sông, cánh chim mà cón thể hiện rõ nét hơn cả quan hình ành "Cóđám mây mùa hạ/Vắt nửa mình sang thu". Hữu Thỉnh dùng động từ “vắt” để gợi ra trong thời điểmgiao mùa, đám mây như kéo dài ra, nhẹ trôi như tấm lụa mềm treo lơ lửng giữabầu trời trong xanh, cao rộng. Mùa ha, mùa thu là 2 đầu bến và đám mây là nhịp cầu vắt qua. Cái tài của Hữu Thỉnh là dùng không gian để miêu tả thời gian, làm hiện rõ ranh giới từ hạ snag thu vốn mong manh trở nên cụ thể, hữu hình. Đám mây là nhịp cầu duyên dáng nối 2 bờ thời gian bằng vẻ đpẹ mềm mại, trữ tình. Qua cách cảm nhận ấy, ta thấy Hữu Thỉnh có một hồn thơ nhạy cảm, yêu thiên nhiên tha thiết, một trí tưởng tượng bay bổng.
LL
21 tháng 12 2021
tham khảo
Ba biểu đồ khí hậu thuộc các kiểu khí hậu sau đây :
+ U-lan-ba-to(Mông Cổ) : Thuộc kiểu khí hậu ôn đới lục địa.
+ E Ri-át (A-rập-xê-út) : thuộc kiểu khí hậu nhiệt đới khô.
+ Y-an-gun (Mi-an-ma) : Thuộc kiểu khí hậu nhiệt đới gió mùa.
– Đặc điểm về nhiệt độ và lượng mưa của mỗi địa điểm :
+ U-lan-Ba-to : Nhiệt độ trung bình năm khoảng 10oC, nhiều tháng dưới 0oC. Lượng mưa trung bình năm 220 mm. Mưa tập trung chủ yếu vào các tháng 5, 6, 7, 8.
+ E Ri-át : nhiệt độ trung bình năm trên 20oC. Lượng mưa trung bình năm 82 mm. Mưa tập trung vào các tháng 1, 2, 3 nhưng rất ít.
+ Y-an-gun : nhiệt độ trung bình năm cao trên 25oC. Lượng mưa trung bình năm trên 2750 mm. Mưa rất nhiều từ tháng 5 đến tháng 10
| Địa điểm | Đặc điểm chế độ nhiệt | Đặc điểm chế độ mưa |
| E Ri-át | Nhiệt độ trung bình năm trên 20oC. | Lượng mưa trung bình năm 82 mm. Mưa tập trung vào các tháng 1, 2, 3 nhưng rất ít. |
| Y-an-gun | Nhiệt độ trung bình năm cao trên 25oC. | Lượng mưa trung bình năm trên 2750 mm. Mưa rất nhiều từ tháng 5 đến tháng 10. |
21 tháng 12 2021
Nhiệt độ cao nhất, thấp nhất, biên độ nhiệt của 3 đó là gì v á.
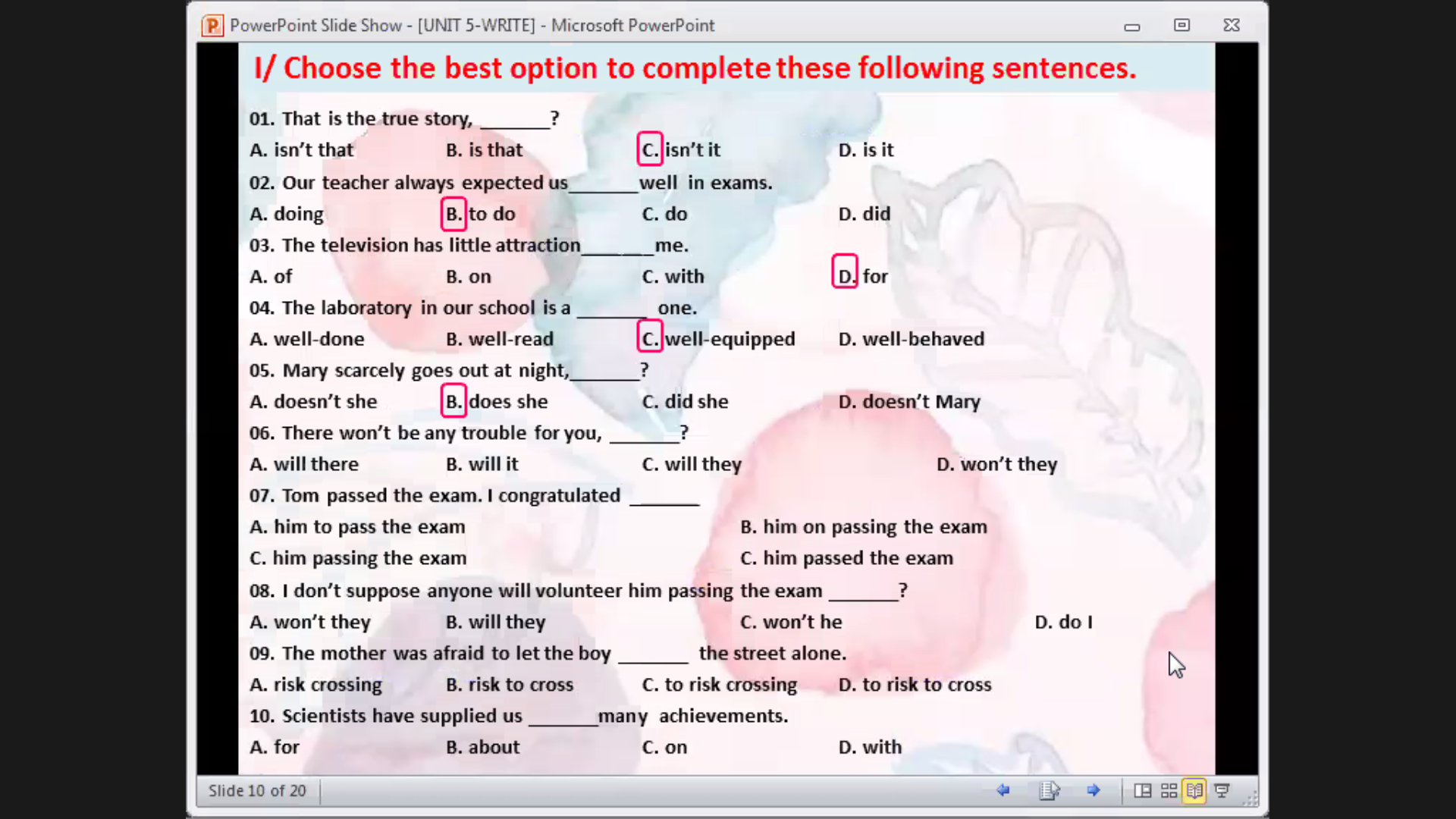
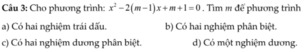
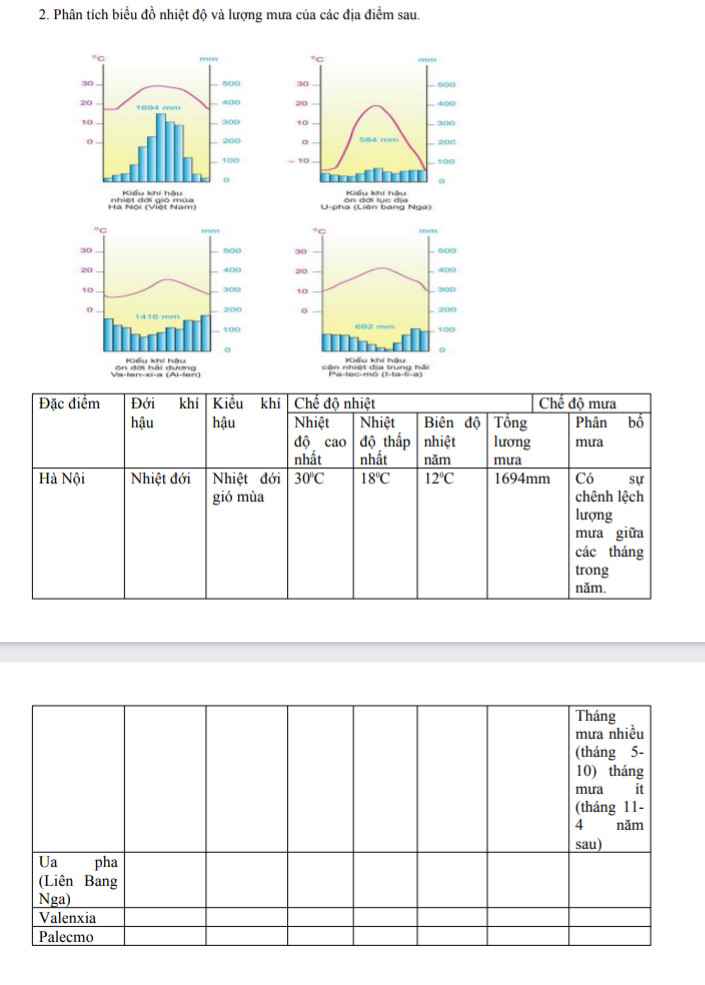
Tham khảo ạ
Học sinh trung học cơ sở nên mặc quần áo bình thường
Mặc quần áo bình thường:
- làm cho học sinh cảm thấy thoải mái.
- cho học sinh tự do lựa chọn (kích cỡ, màu sắc, và kiểu dáng, v.v)
- tạo cho học sinh cảm giác tự tin khi diện những bộ quần áo yêu thích.
- làm cho trường học đầy màu sắc và sống động