Chứng minh các đẳng thức
128.912=1816
giai giùm nha lớp 7 đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
UI
8 tháng 9 2019
Bai nay phai co dieu kien a,b >0 nha ban
Ap dung bdt \(ab\le\frac{\left(a+b\right)^2}{4}< \frac{1}{4}\) dau nho hon la do gia thiet nha ban
Ap dung bdt Cosi cho 2 so ko am
ta co A= \(ab+\frac{1}{16ab}+\frac{15}{16ab}>2\sqrt{ab.\frac{1}{16ab}}+\frac{15}{16.\frac{1}{4}}=2.\frac{1}{4}+\frac{15}{4}=\frac{17}{4}\)
Study well
18 tháng 8 2019
câu trên không có điều kiện các bạn nhé ! chỉ có thế thôi!
KV
25 tháng 12 2023
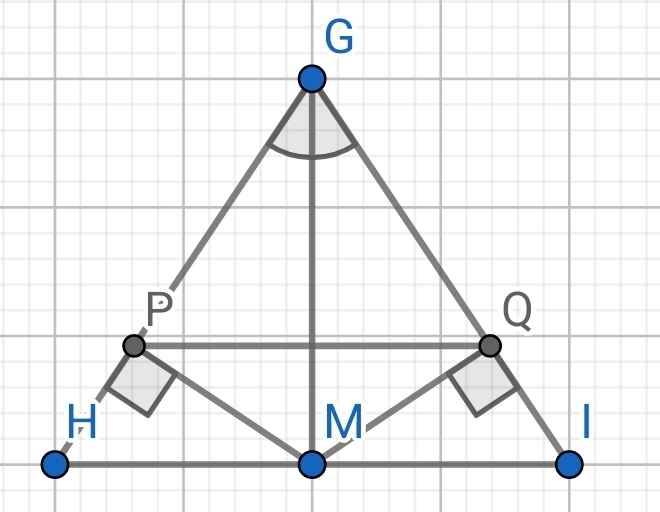a) Do GM là tia phân giác của ∠HGI (gt)
⇒ ∠HGM = ∠IGM
Xét ∆GHM và ∆GIM có:
GH = GI (do ∆GHI cân tại G)
∠HGM = ∠IGM (cmt)
GM là cạnh chung
⇒ ∆GHM = ∆GIM (c-g-c)
b) Do ∆GHM = ∆GIM (cmt)
⇒ HM = IM (hai cạnh tương ứng)
Do ∆GHM = ∆GIM (cmt)
⇒ ∠GMH = ∠GMI (hai góc tương ứng)
Mà ∠GMH + ∠GMI = 180⁰ (kề bù)
⇒ ∠GMH = ∠GMI = 180⁰ : 2 = 90⁰
⇒ GM ⊥ HI
c) Do ∠HGM = ∠IGM (cmt)
⇒ ∠PGM = ∠QGM
Xét hai tam giác vuông: ∆GMP và ∆GMQ có:
GM là cạnh chung
∠PGM = ∠QGM (cmt)
⇒ ∆GMP = ∆GMQ (cạnh huyền góc nhọn)
⇒ MP = MQ (hai cạnh tương ứng)
⇒ ∆MPQ cân tại M
7 tháng 3 2022
Thì bạn lấy một ví dụ đơn giản là A đi qua nhà B thì có hai cách là đi thẳng hoặc đi vòng. Nếu đi vòng thì độ dài quãng đường sẽ lớn hơn đi thẳng nên ta có bất đẳng thức tam giác
7 tháng 3 2022
Thì bạn lấy một ví dụ đơn giản là A đi qua nhà B thì có hai cách là đi thẳng hoặc đi vòng. Nếu đi vòng thì độ dài quãng đường sẽ lớn hơn đi thẳng nên ta có bất đẳng thức tam giác
7 tháng 3 2022
Thì bạn lấy một ví dụ đơn giản là A đi qua nhà B thì có hai cách là đi thẳng hoặc đi vòng. Nếu đi vòng thì độ dài quãng đường sẽ lớn hơn đi thẳng nên ta có bất đẳng thức tam giác
\(12^8.9^{12}=18^{16}\)
\(12^{2.4}.9^{3.4}=18^{4.4}\)
\(\left(12^2\right)^4.\left(9^3\right)^4=\left(18^4\right)^4\)
\(\Rightarrow12^2.9^3=18^4\)
\(12^2=18^4:9^3\)
\(12^2=144=12^2\)
Vậy đẳng thức đc chứng minh
cái này lớp 6 có rùi!