Cho đường tròn (O), hai dây MN=PQ cắt nhau tại A nằm ngoài (O). Gọi E,F lần lượt là trung điểm MN và PQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi E là giao của AO và MN
MN là đường trung bình của ΔABC
=>MN//BC
=>MN vuông góc AO tại E
PA^2=PE^2+AE^2
=AN^2-EN^2+OP^2-EO^2
=NC^2-EN^2+PQ^2+QO^2-EO^2
=NO^2-R^2+PQ^2+R^2-NO^2
=PQ^2
=>PA=PQ

4) Gọi P, Q lần lượt là tâm của các đường tròn ngoại tiếp tam giác MBK, tam giác MCK và E là trung điểm của đoạn PQ. Vẽ đường kính ND của đường tròn (O) . Chứng minh ba điểm D, E, K thẳng hàng.

Vì N là điểm chính giữa cung nhỏ BC nên DN là trung trực của BC nên DN là phân giác B D C ^
Ta có K Q C ^ = 2 K M C ^ (góc nọi tiếp bằng nửa góc ở tâm trong dường tròn (Q))
N D C ^ = K M C ^ (góc nội tiếp cùng chắn cung N C ⏜ )
Mà B D C ^ = 2 N D C ^ ⇒ K Q C ^ = B D C ^
Xét 2 tam giác BDC & KQC là các các tam giác vuông tại D và Q có hai góc ở ⇒ B C D ^ = B C Q ^ do vậy D, Q, C thẳng hàng nên KQ//PK
Chứng minh tương tự ta có ta có D, P, B thẳng hàng và DQ//PK
Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng (điều phải chứng minh).

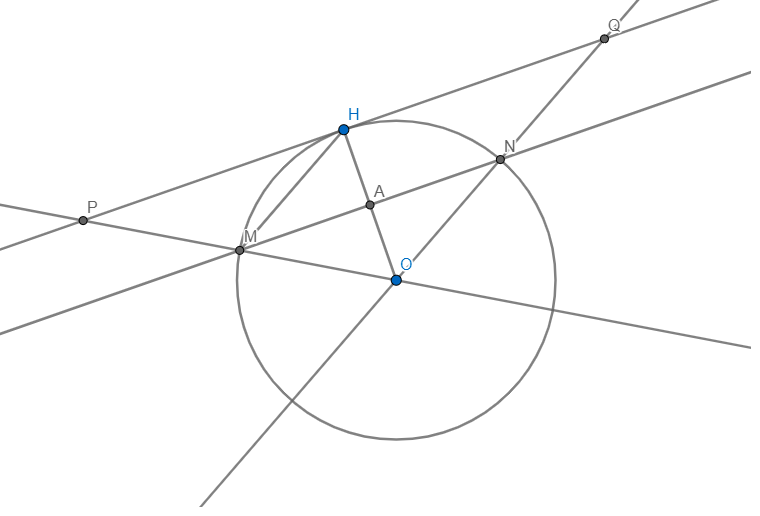
MN cắt OH tại A.
Vì MN là trung trực \(\Rightarrow MN\bot OH\) và A là trung điểm OH
mà \(PQ\bot OH\) \(\Rightarrow PQ\parallel MN\)
Xét \(\Delta OHQ\) có A là trung điểm OH và \(AN\parallel HQ\)
\(\Rightarrow N\) là trung điểm OQ
Tương tự \(\Rightarrow M\) là trung điểm OP
\(\Rightarrow MN\) là đường trung bình tam giác OPQ
\(\Rightarrow PQ=2MN\)
Vì MN là trung trực OH \(\Rightarrow MH=MO=OH\left(=R\right)\Rightarrow\Delta MOH\) đều
\(\Rightarrow MA=sinMHA.MH=sin60.R=\dfrac{\sqrt{3}}{2}R\Rightarrow MN=\sqrt{3}R\)
\(\Rightarrow PQ=2\sqrt{3}R\)
Đề bài yêu cầu gì vậy bạn?