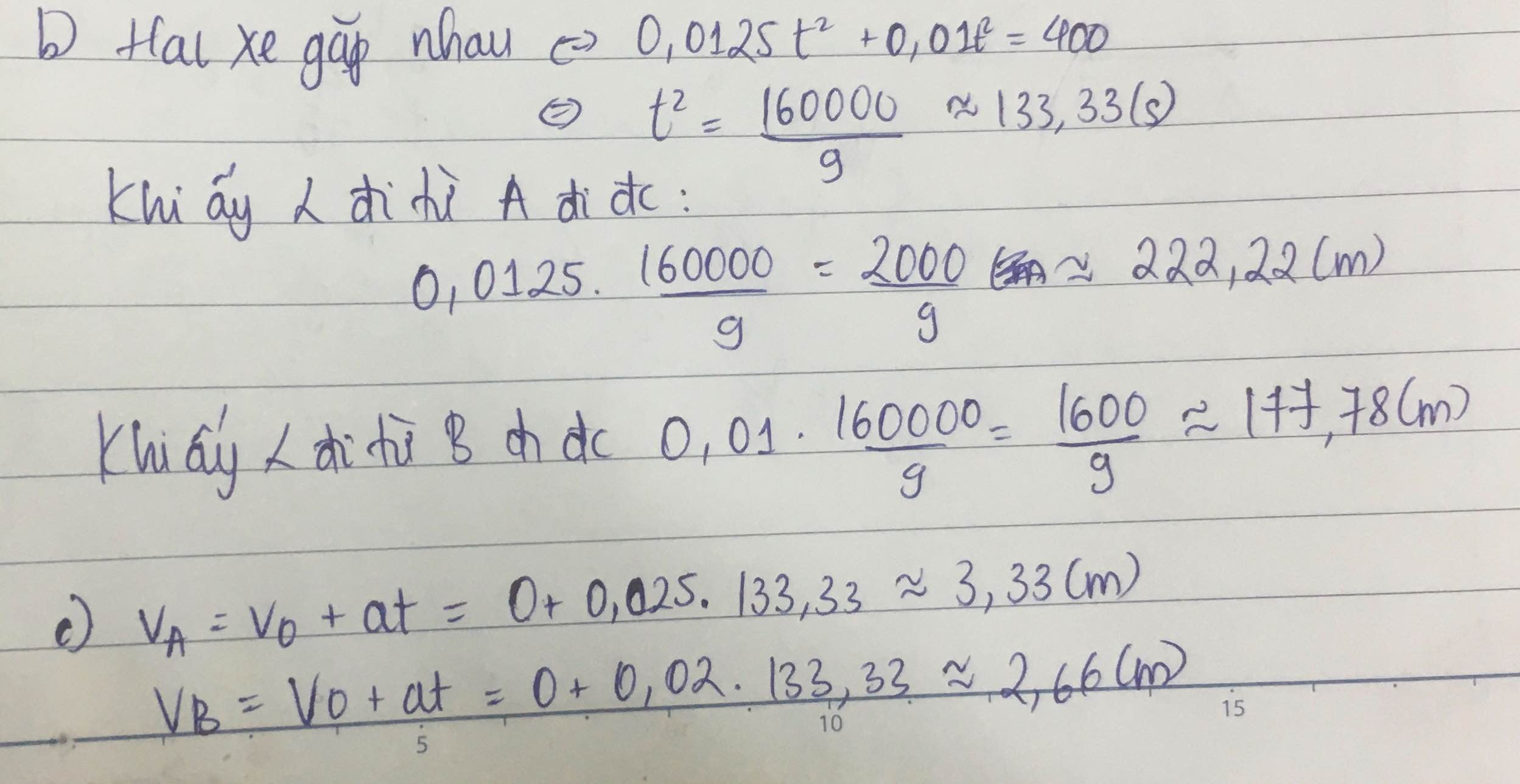Bài 8. Lúc 7h một ôtô bắt đầu xuất phát từ A với gia tốc a1=0.1m/s2. 10s sau từ điểm B cách A 50m về phía
trước một ôtô khác cũng bắt xuất phát với gia tốc a2=0,1m/s2 và chạy cùng chiều với xe thứ nhất.
a) Viết phương trình chuyển động của mỗi xe
b) Xác định thời và vị trí hai xe đuổi kịp nhau
Đ/s. sau 30s;cách A 150m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi G là vị trí hai ô tô gặp nhau
Đối với ô tô đi từ A:
\(AG=\dfrac{1}{2}a_1t^2+v_0t=\dfrac{1}{2}.1.t^2-10t=\dfrac{1}{2}t^2-10t\)
Đối với ô tô đi từ B:
\(BG=\dfrac{1}{2}a_2t^2=\dfrac{1}{2}.2.t^2=t^2\)
Lại có: \(AG-BG=AB\)
\(\Leftrightarrow\dfrac{1}{2}t^2-t^2+10t=50\)
\(\Leftrightarrow t=10\left(s\right)\)
Vị trí hai ô tô gặp nhau cách A một khoảng: \(AG=\dfrac{1}{2}t^2+10t=150\left(m\right)\)
Và gặp nhau sau 10s kể từ lúc chuyển động

a. Chọn gốc tọa độ A , gốc thời gian là lúc hai xe xuất phát, chiều dương từ A đến B.
Phương trình xe 1: \(x_1=x_{0_1}+v_1t=30t\)
Phương trình xe 2: \(x_2=x_{0_2}+v_2t=10-40t\)
b. Khi hai xe gặp nhau thì: \(x_1=x_2\Leftrightarrow30t=10-40t\Rightarrow t=\dfrac{1}{7}\left(h\right)\)
Vị trí hai xe gặp nhau cách A: \(s=x_1=30.\dfrac{1}{7}=\dfrac{30}{7}\left(km\right)\)

Khi hai xe máy gặp nhau thì x 1 = x 2 , nghĩa là:
1,25. 10 - 2 t 2 = 400 + 1,0. 10 - 2 t 2 hay ⇒ t = 400 s
Như vậy sau thời gian t = 400 s = 6 phút 40 giây kể từ lúc xuất phát thì hai xe đuổi kịp nhau.
Thay vào ta tìm được vị trí hai xe đuổi kịp nhau cách A đoạn x1 = 1,25. 10 - 2 . 400 2 = 2000 m = 2 km

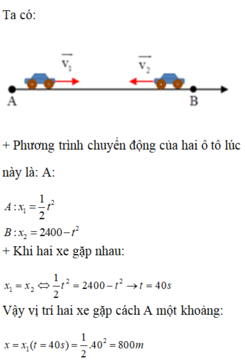
a) Phương trình chuyển động:
* Vật thứ nhất: x 1 = 5 t (m).
* Vật thứ hai: x 2 = 50 − t 2 (m).
b) Khi gặp nhau thì x 1 = x 2 ⇔ 5 t = 50 − t 2 hay t 2 + 5 t − 50 = 0 (*)
Giải phương trình (*) ta được: t 1 = 5 s; t 2 = − 10 s (loại).
Vị trí gặp nhau: x 1 = x 2 = 5.5 = 25 m.
Vậy hai vật gặp nhau tại thời điểm t = 5 s, tại vị trí cách A 25m.
c) Khi hai vật có vận tốc bằng nhau thì v 1 = v 2 = 5 m/s.
Phương trình vận tốc của vật thứ 2: v 2 = 2 t = 5 ⇒ t = 2 , 5 s .