Tìm Giá trị nhỏ nhất : C=7x2-7x-3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
Lời giải:
$A=x^4-4x^3+7x^2-12x+75$
$=(x^2-2x)^2+3x^2-12x+75$
$=(x^2-2x)^2+3(x^2-4x+4)+63$
$=(x^2-2x)^2+3(x-2)^2+63\geq 63$
Vậy $A_{\min}=63$. Giá trị này đạt tại $x^2-2x=x-2=0$
$\Leftrightarrow x=2$
NK
1
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2021
\(A=\left(x^4-4x^3+4x^2\right)+\left(3x^2-12x+12\right)+63\)
\(A=x^2\left(x^2-4x+4\right)+3\left(x^2-4x+4\right)+63\)
\(A=\left(x^2+3\right)\left(x-2\right)^2+63\ge63\)
\(A_{min}=63\) khi \(x=2\)
TL
0
PT
1
CM
16 tháng 12 2019
- Tính giá trị của hàm số tại các điểm trên (cả hai đầu mút) và so sánh.
Cách giải:
Ta có:
CM
18 tháng 9 2019
Chọn A
Hàm số y =
x
3
-
7
x
2
+
11
x
-
2
liên tục trên đoạn [0;2] và có 
Ta có 
TT
0
TD
0
25 tháng 6 2015
\(7x^2-8x=7\left(x^2-\frac{8}{7}\right)=7\left(x^2-2.x.\frac{4}{7}+\frac{16}{49}-\frac{16}{49}\right)\)
\(=7\left[\left(x-\frac{4}{9}\right)^2-\frac{16}{49}\right]=7\left(x-\frac{4}{9}\right)^2-\frac{16}{7}\)
Vì \(\left(x-\frac{4}{9}\right)^2\ge0\Leftrightarrow7\left(x-\frac{4}{9}\right)^2\ge0\Leftrightarrow7\left(x-\frac{4}{9}\right)^2-\frac{16}{7}\ge-\frac{16}{7}\)
VẬy GTNN của bt là -16/7 khi x -4/9 = 0=> x = 4/9
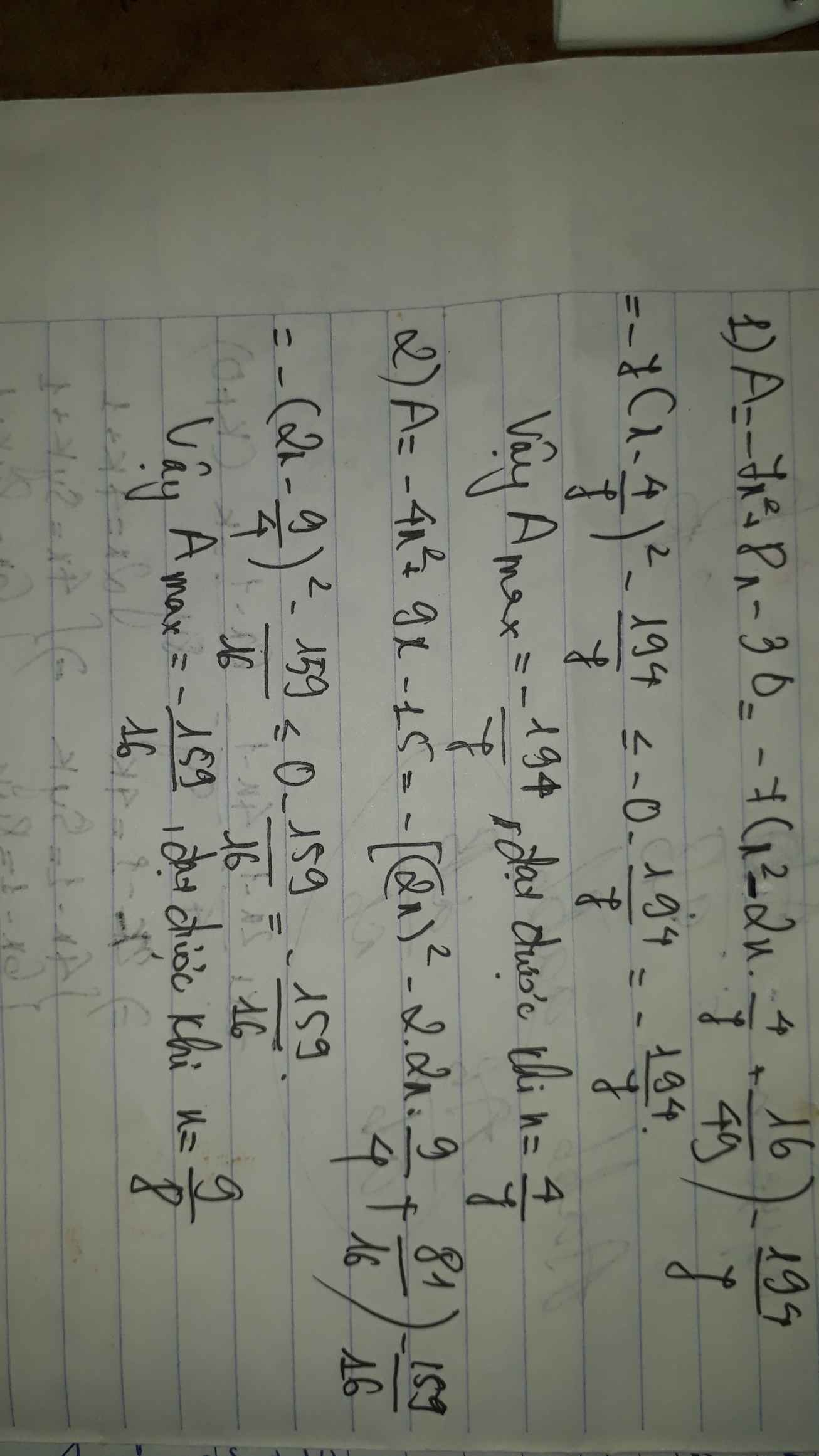
C= \(\left(\sqrt{7}x\right)^2-2\sqrt{7}x.\sqrt{7}+7-7-3=\left(\sqrt{7}x-\sqrt{7}\right)^2-10\)
vi \(\left(\sqrt{7}x-\sqrt{7}\right)^2\)> 0
-> \(\left(\sqrt{7}x-\sqrt{7}\right)^2\)-10 > -10
vay C dat GTNN la -10 khi x=1