Cho hai hộp, mỗi hộp chứa các viên bi trắng và đen. Tổng số các viên bi trong hai hộp là 25. Từ mỗi hộp, lấy ra ngẫu nhiên 1 viên bi. Tìm xác suất để 2 viên bi lấy ra khác màu nếu biết hộp nào nhiều bi hơn thì số bi đen nhiều hơn và xác suất để hai viên lấy ra cùng màu đen là 0,42
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 10 2018
Chọn B
Lời giải.
Giả sử hộp thứ nhất có x viên bi, trong đó có a viên bi đen;
hộp thứ hai có y viên bi, trong đó có b viên bi đen
Điều kiện: x , y , a , b là các số nguyên dương và
Theo giả thiết, ta có
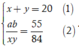
Từ ( 2 ) ⇔ 55 x y = 84 a b
suy ra xy chia hết cho 84
Mặt khác, ta có
nên xy = 84 (3)
Từ (1) và (3), ta được x = 14 y = 6
Từ (3) và (2), suy ra ab = 55 nên a là ước của 55
Lại có 55 6 ≤ 55 b = a ≤ 14 nên a = 11
Với a= 11, ta được b = 5
Vậy xác suất để được 2 bi trắng là
CM
28 tháng 9 2017
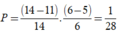
Chọn D
Giả sử hộp 1 có viên bi, trong đó có a viên bi đen.
Hộp 2 có y viên bi, trong đó có b viên bi đen.
x, y, a, b là những số nguyên dương, 
)
Từ giả thiết x + y = 20,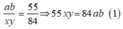 
Từ đó ta có xy chia hết cho 84
Mặt khác 
suy ra xy = 84 ta được x = 14, y = 6
Thay vào (1) ta được ab = 55 nên a là ước của 55. Do a ≤ 14 nên a = 11 suy ra b = 5.
Vậy xác suất để lấy được 2 bi trắng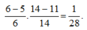 
CM
9 tháng 4 2017
Chọn A
Lời giải
Không gian mẫu là số sách chọn ngẫu nhiên mỗi hộp 1 viên bi
Số phần tử của không gian mẫu là Ω = C 15 1 . C 18 1
Gọi X là biến cố "2 viên bi lấy ra từ mỗi hộp có cùng màu"
Ta có các kết quả thuận lợi cho biến cố X như sau
● Hộp A lấy ra 1 bi trắng và hộp B lấy ra 1 bi trắng, có C 4 1 . C 7 1 cách
● Hộp A lấy ra 1 bi đỏ và hộp B lấy ra 1 bi đỏ, có C 5 1 . C 6 1 cách
● Hộp A lấy ra 1 bi xanh và hộp B lấy ra 1 bi xanh, có C 6 1 . C 5 1 cách
Suy ra số phần tử của biến cố
Vậy xác suất cần tính
P ( X ) = Ω x Ω = 44 135
CM
13 tháng 10 2018
Chọn B.
Số cách lấy 7 viên bi từ hộp là C 35 7
Số cách lấy 7 viên bi không có viên bi đỏ là C 20 7 .
Số cách lấy 7 viên vi có ít nhất 1 viên đỏ là C 55 7 - C 20 7 xác suất là C 55 7 - C 20 7 C 55 7 .
CM
24 tháng 7 2019
Gọi A là biến cố: “trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ.”
Trong hộp có tất cả: 5+ 15 + 35 = 55 viên bi
- Số phần tử của không gian mẫu: Ω = C 55 7 .
- A ¯ là biến cố: “trong số 7 viên bi được lấy ra không có viên bi màu đỏ nào.”
=> n A ¯ = C 20 7 .
Vì A và A ¯ là hai biến cố đối nên: n A = Ω − n A ¯ = C 55 7 − C 20 7 .
Xác suất để trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ là P A = C 55 7 − C 20 7 C 55 7 .
Chọn đáp án B.
CM
24 tháng 8 2019
Đáp án D.
1. Tìm không gian mẫu.
Bạn Hà lấy ngẫu nhiên 2 viên bi có C 6 2 trường hợp.
Bạn Lâm lấy ngẫu nhiên 2 viên bi trong 4 viên còn lại có C 4 2 trường hợp.
Bạn Anh lấy 2 viên bi còn lại có 1 trường hợp.
Vậy n Ω = C 6 2 . C 4 2 = 90 .
2. Gọi A là biến cố “Hai viên bi bạn Anh lấy ra có cùng màu”.
Trường hợp 1: Hai viên bi bạn Anh lấy ra có cùng màu đỏ thì số trường hợp xảy ra là C 4 2 . C 2 2 .1 = 6 .
Trường hợp 2: Hai viên bi bạn Anh lấy ra có cùng màu xanh thì số trường hợp xảy ra là C 4 2 . C 2 2 .1 = 6
Trường hợp 3: Hai viên bi bạn Anh lấy ra có cùng màu vàng thì số trường hợp xảy ra là C 4 2 . C 2 2 .1 = 6 .
⇒ n A = 6.3 = 18 ⇒ P A = n A n Ω = 18 90 = 1 5
TA
19 tháng 12 2020
Hộp 1 có 9 viên, hộp 2 có 9 viên, lấy ở mỗi hộp 1 viên.
\(\Rightarrow n(Ω)=(C_{9}^{1})^2=81\)
A: "Hai viên bi chọn được cùng màu".
TH1: cùng màu vàng: \(C_{6}^{1} .C_{5}^{1} =30\)
TH2: cùng màu đỏ: \(C_{3}^{1} .C_{4}^{1}=12\)
\(\Rightarrow n(A)=30+12=42\)
\(\Rightarrow P(A) =\dfrac{n(A)}{n(Ω)}=\dfrac{42}{81}=\dfrac{14}{27}\).
TA
19 tháng 12 2020
Hộp 1 có 9 viên, hộp 2 có 9 viên, lấy ở mỗi hộp 1 viên.
\(\Rightarrow n(Ω)=(C_{9}^{1})^2=81\)
A: "Hai viên bi chọn được cùng màu".
TH1: cùng màu vàng: \(C_{6}^{1} .C_{5}^{1} =30\)
TH2: cùng màu đỏ: \(C_{3}^{1} .C_{4}^{1}=12\)
\(\Rightarrow n(A)=30+12=42\)
\(\Rightarrow P(A) =\dfrac{n(A)}{n(Ω)}=\dfrac{42}{81}=\dfrac{14}{27}\).