A B C D d c a b cho tam giác ABC \(\simeq\) ACD, góc C vuông, góc ABC vuôngCMR:...
Đọc tiếp
cho tam giác ABC \(\simeq\) ACD, góc C vuông, góc ABC vuông
CMR: 1/d2=1/a2+1/b2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 4 2019
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
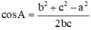
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
9 tháng 7 2021
Sửa đề: cắt AB tại D.
a) Sửa đề: ΔACD=ΔECD
Xét ΔACD vuông tại A và ΔECD vuông tại E có
CD chung
\(\widehat{ACD}=\widehat{ECD}\)(CD là tia phân giác của \(\widehat{ACE}\))
Do đó: ΔACD=ΔECD(Cạnh huyền-góc nhọn)
b) Ta có: ΔACD=ΔECD(cmt)
nên DA=DE(Hai cạnh tương ứng)
Xét ΔDAE có DA=DE(cmt)
nên ΔDAE cân tại D(Định nghĩa tam giác cân)
V
1
15 tháng 1 2021
Ta có: \(a\left(a^2-b^2\right)=c\left(b^2-c^2\right)\Leftrightarrow a^3+c^3=b^2c+b^2a\)
\(\Leftrightarrow\left(a+c\right)\left(a^2-ac+c^2\right)=b^2\left(c+a\right)\Leftrightarrow b^2=a^2-ac+c^2\).
Theo định lý hàm cos: \(b^2=a^2+c^2-2cos\widehat{B}.ac\).
Do đó \(cos\widehat{B}=\dfrac{1}{2}\) hay \(\widehat{B}=60^o\).
Tam giác \(ACD\)vuông tại \(C\)đường cao \(CB\):
\(cd=ab\)
\(\Leftrightarrow c^2d^2=a^2b^2\)
\(\Leftrightarrow\frac{1}{d^2}=\frac{c^2}{a^2b^2}=\frac{a^2+b^2}{a^2b^2}=\frac{1}{a^2}+\frac{1}{b^2}\).