s^3 - 15s + 14 =0
GIẢI Phương trình dùm mình đi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
KK
2
Những câu hỏi liên quan
KK
2
23 tháng 12 2021
#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
DH
8 tháng 3 2023
- toạ độ điểm A(0,3) => vecto ah (1;-2)
mà vecto ah vuông góc vecto bc => vecto chỉ phương ah = vecto pháp tuyến bc = (1;-2)
B thuộc AB => 5xb - 2yb = -6
C thuộc AC => 4xc + 7yc = 21
xc - xb = 1
yc - yb = -2
giải hệ 4 pt => toạ độ điểm B, C
- Có vecto pháp tuyến, điểm B(C) => viết phương trình đường thẳng
29 tháng 10 2023
\(x^3-3x+2-2m=0\)
=>\(2m=x^3-3x+2\)
Chúng ta sẽ vẽ đồ thị \(y=x^3-3x+2\)
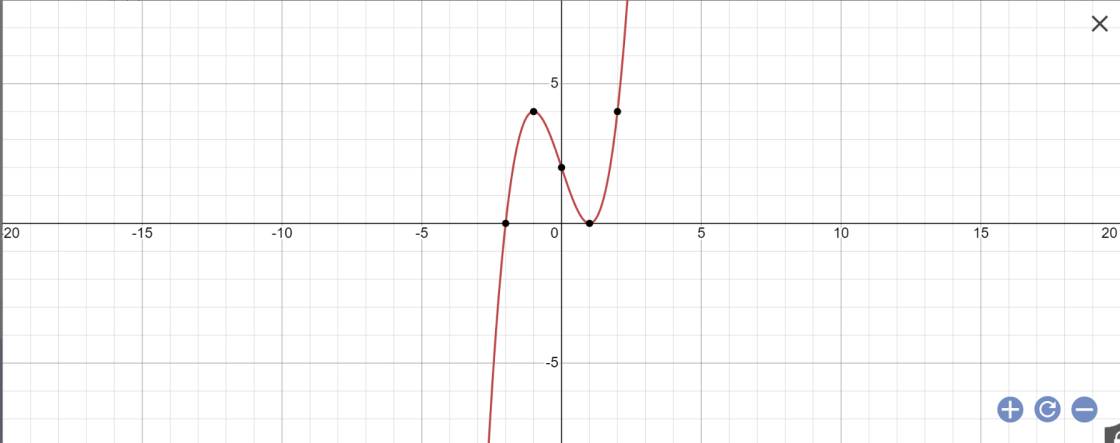
Trên đồ thị, chúng ta sẽ thấy khi \(y\in\left(0;4\right)\) thì \(y=x^3-3x+2\) sẽ cho 3 nghiệm phân biệt
=>\(2m\in\left(0;4\right)\)
=>\(m\in\left(0;2\right)\)
=>Chọn B
13 tháng 5 2021
`m=5`
`=>-20x+5-3=0`
`=>-20x+2=0`
`=>x=-1/10=>m=5` pt có nghiệm
Nếu `m ne 5=>` pt trên là pt bậc 2
ĐK để pt bậc 2 có nghiệm
`=>Delta'>0`
`<=>4m^2-(m-2)(m-5)>0`
`<=>4m^2-(m^2-7m+5)>0`
`<=>3m^2+7m-5>0`
`<=>m^2+7/3m-5/3>0`
`<=>(m+7/6)^2-109/36>0`
`<=>` \(\left[ \begin{array}{l}m>\dfrac{\sqrt{109}-7}{6}\\m<\dfrac{-\sqrt{109}-7}{6}\end{array} \right.\)
24 tháng 2 2021
2x2 - ( m + 4 )x + m = 0
Δ = b2 - 4ac = ( m + 4 )2 - 8m = m2 + 8m + 16 - 8m = m2 + 16
Vì m2 + 16 ≥ 16 > 0 ∀ m => Δ ≥ 16 > 0
Vậy phương trình luôn có nghiệm ( đpcm )
10 tháng 3 2016
c) tim x1 và x2 theo ct;
x1= 16 +can denta ....tu lam
d) c/a <0
lam dc roi chu
H
12 tháng 5 2021
a)
\(4FeS_2 + 11O_2 \xrightarrow{t^o} 2Fe_2O_3 + 8SO_2\\ 2SO_2 + O_2 \xrightarrow{t^o,xt} 2SO_3\\ SO_3 + H_2O \to H_2SO_4\\ Fe_2O_3 + 3H_2SO_4 \to Fe_2(SO_4)_3 + 3H_2O\\ Fe_2(SO_4)_3 + 6KOH \to 2Fe(OH)_3 + 3K_2SO_4\\ Fe_2(SO_4)_3 + 3BaCl_2 \to 3BaSO_4 + 2FeCl_3\)
b)
\(3Mg + 4H_2SO_4 \to 3MgSO_4 + S + 4H_2O\\ S + Mg \xrightarrow{t^o} MgS\\ MgS + 2HCl \to MgCl_2 + H_2S\\ H_2S + \dfrac{1}{2}O_2 \xrightarrow{t^o} S + H_2O\\ S + O_2 \xrightarrow{t^o} SO_2\\ SO_2 + NaOH \to NaHSO_3\\ NaHSO_3 + NaOH \to Na_2SO_3 + H_2O\\ Na_2SO_3 + H_2SO_4 \to Na_2SO_4 + SO_2 + H_2O\\ Na_2SO_4 + BaCl_2 \to BaSO_4 + 2NaCl\)
7 tháng 10 2021
Đk: \(x\ge1\)
\(\Leftrightarrow4\left(2\sqrt{x-1}-1\right)+\left(4x-5\right)\left(x+2\right)=0\)
\(\Leftrightarrow\dfrac{4\left(4x-5\right)}{2\sqrt{x-1}+1}+\left(4x-5\right)\left(x+2\right)=0\)
\(\Leftrightarrow\left(4x-5\right)\left(\dfrac{4}{2\sqrt{x-1}+1}+x+2\right)=0\)
\(\Leftrightarrow x=\dfrac{5}{4}\)(Dễ thấy ngoặc to lớn hơn 0 với \(x\ge1\))
s3-15s+14=0
=>s3-s-14s+14=0
=>s(s2-1)-14(s-1)=0
=>s(s-1)(s+1)-14(s-1)=0
=>[s(s+1)-14](s-1)=0
=>s-1=0=>s=1
hoặc s(s+1)-14=0
=>s(s+1)=14 (vô lí)
vậy s=1
s3-15s+14=0
<=>(s3-s)-(14s-14)=0
<=>s(s-1)(s+1)-14(s-1)=0
<=>(s-1)(s2+s-14)=0
<=>s-1=0<=>s=1
hoặc s2+s-14=0
<=>(s+1/2)2-14,25=0
<=>(s+1/2)2=14,25
<=>\(s+\frac{1}{2}=_-^+\sqrt{14,25}\Leftrightarrow s=_-^+\sqrt{14,25}-\frac{1}{2}\)