Cho góc aob có số đo bằng 120 độ. Gọi om là tia phân giác của góc aob
A, tính số đo góc aom
B, gọi ox là tia đối của của tia ob, chứng tỏ oa là tia phân giác của góc xom
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 8 2021
a) Vì Oa⊥Ox⇒xOa=90o;Ob⊥Oy⇒yOb=90oOa⊥Ox⇒xOa=90o;Ob⊥Oy⇒yOb=90o
Ta có: xOa + aOy = xOy
=> 90o + aOy = xOy (1)
Lại có: xOb + bOy = xOy
=> xOb + 90o = xOy (2)
Từ (1) và (2) => aOy = xOb
b) Vì Om là phân giác của aOb nên bOm=mOa=aOb2bOm=mOa=aOb2
Lại có: aOy = xOb (theo câu a)
=> aOy + mOa = bOm + xOb
=> mOy = xOm
=> Om là tia phân giác của aOb (đpcm)
3 tháng 4 2021
a)Ta có: hai tia On và Óc cùng thuộc một nửa mặt phẳng chứa tia Oa
Mà aOb<aOc(60o <120o)
=} Tia Ob nằm giữa hai tia Oa và Ob (1)
=} aOb + boc=aOc
Mà aOb =60o,aOc=120
=}Boc=120o-60o=60o(2)
Vậy bOc=60o
3 tháng 4 2021
a) Trên cùng một nửa mặt phẳng bờ chứa tia Oa, ta có: \(\widehat{aOb}< \widehat{aOc}\left(60^0< 120^0\right)\)
nên tia Ob nằm giữa hai tia Oa và Oc
\(\Leftrightarrow\widehat{aOb}+\widehat{bOc}=\widehat{aOc}\)
\(\Leftrightarrow\widehat{bOc}+60^0=120^0\)
hay \(\widehat{bOc}=60^0\)
Vậy: \(\widehat{bOc}=60^0\)
HM
2 tháng 4 2019
a) Trên cùng một nửa mặt phẳng có bờ chứa tia Ox có xOy<xOz (60 < 150) nên tia Oy nằm giữa hai tia Oz và Ox, ta có:
zOy + yox = zOx
zOy+ 60 = 150
zOy = 150-60
zOy = 90
Vậy xOy = 90
b) Vì Ot là tia đối của tia Oz nên zOt=180
Trên cùng một nửa mặt phẳng có bờ chứa tia Oz có zOx<xOt (150 < 180) nên tia Oz nằm giữa hai tia Ox và Ot, ta có:
zOx +xOt =zOt
150 +xOt=180
xOt=180 - 150
xOt= 30
Vậy xOt = 30
CM
5 tháng 5 2018
a. Ta có:
O A ⊥ O C ( G T ) ⇒ A O C ^ = 90 ° O D ⊥ O B ( G T ) ⇒ D O B ^ = 90 ° A O D ^ + C O D ^ = A O C ^ = 90 ° B O C ^ + C O D ^ = D O B ^ = 90 °
⇒ A O D ^ = B O C ^ (Cùng phụ C O D ^ )
b. Ta có:
A O D ^ + B O D ^ = A O B ^ ⇒ A O D ^ + 90 ° = 130 ° ⇒ A O D ^ = 130 ° − 90 ° ⇒ A O D ^ = 40 °
Mà A O D ^ + C O D ^ = 90 ° ( C M T )
40 ° + C O D ^ = 90 ° C O D ^ = 50 °
c. OM là tia phân giác của A O B ^ nên:
A O M ^ = B O M ^ = A O B ^ 2 = 65 °
A O D ^ + D O M ^ = A O M ^ 40 ° + D O M ^ = 65 ° D O M ^ = 25 °
Tương tự ta tìm được C O M ^ = 25 °
Do đó C O M ^ = D O M ^ ( = 25 ° )
Vậy OM là tia phân giác của C O D ^
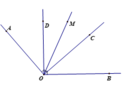
Tham khảo nha! Cách này hơi dài ạ
a, Có Om là tia phân giác của góc aOb => Om nằm giữa Oa và Ob; góc aOm = góc mOb = aOb/2 = 120 độ/2 = 60 độ
b, Có mOb và mOx là 2 góc kề bù
=>mOb + mOx = 180 độ
=>60 độ + mOx= 180 độ
=> mOx = 120 độ
Trên nửa mp bờ chứa tia Ox có:
Góc mOa = 60 độ
Góc mOx = 120 độ
=>mOa < mOx => tia Oa nằm giữa 2 tia Ox và Om
=> mOa + aOx = mOx
=> aOx=60 độ
Có Oa nằm giữa Ox và Om; mOa=aOx= 60 độ
=> Tia Oa là tia phân giác của góc xOm
a) Ta có: Om là tia phân giác của \(\widehat{aOb}\)(gt)
nên \(\widehat{aOm}=\dfrac{\widehat{aOb}}{2}=\dfrac{120^0}{2}=60^0\)