giúp mình bài 8 với ạ
Cảm ơn nhiều 😀
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
giúp mình bài 7, bài 8 với ạ, cảm ơn nhiều
6 tháng 2 2022
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
b: Ta có: ΔABE=ΔACD
nên BE=CD
c: Xét ΔDBC và ΔECB có
DB=EC
DC=EB
BC chung
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{KCB}=\widehat{KBC}\)
hay ΔKBC cân tại K
d: Xét ΔABK và ΔACK có
AB=AC
BK=CK
AK chung
Do đó: ΔABK=ΔACK
Suy ra: \(\widehat{BAK}=\widehat{CAK}\)
hay AK là tia phân giác của góc BAC
HN
3
AH
Akai Haruma
Giáo viên
2 tháng 1
Câu 8:
a. Với $x,y$ là số nguyên thì $x, y-3$ cũng là số nguyên. Mà $x(y-3)=15$ nên ta có các TH:
TH1: $x=1, y-3=15\Rightarrow x=1; y=18$ (tm)
TH2: $x=-1, y-3=-15\Rightarrow x=-1; y=-12$ (tm)
TH3: $x=15; y-3=1\Rightarrow x=15; y=4$ (tm)
TH4: $x=-15; y-3=-1\Rightarrow x=-15; y=2$ (tm)
TH5: $x=3, y-3=5\Rightarrow x=3; y=8$ (tm)
TH6: $x=-3; y-3=-5\Rightarrow x=-3; y=-2$ (tm)
TH7: $x=5; y-3=3\Rightarrow x=5; y=6$ (tm)
TH8: $x=-5; y-3=-3\Rightarrow x=-5; y=0$ (tm)
AH
Akai Haruma
Giáo viên
2 tháng 1
Câu 8:
b.
$xy-2y+3(x-2)=7$
$\Rightarrow y(x-2)+3(x-2)=7$
$\Rightarrow (x-2)(y+3)=7$
Do $x,y$ nguyên nên $x-2, y+3$ nguyên. Mà tích của chúng bằng $7$ nên ta có các TH sau:
TH1: $x-2=1, y+3=7\Rightarrow x=3; y=4$ (tm)
TH2: $x-2=-1; y+3=-7\Rightarrow x=1; y=-10$ (tm)
TH3: $x-2=7, y+3=1\Rightarrow x=9; y=-2$ (tm)
TH4: $x-2=-7; y+3=-1\Rightarrow x=-5; y=-4$ (tm)
FG
1
15 tháng 5 2022
\(\Leftrightarrow x\left(\dfrac{1}{2}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{14}\right)=\dfrac{1}{21}\)
\(\Leftrightarrow x\cdot\dfrac{2}{7}=\dfrac{1}{21}\)
hay \(x=\dfrac{1}{21}:\dfrac{2}{7}=\dfrac{1}{6}\)
LN
17 tháng 1 2019
số góc chung tạo được là: 10.(10-1):2=45(góc)
vậy số góc chung là 45 góc
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 8 2023
Các số được điền vào các ô theo thứ tự từ trái sang phải là:
-1; - \(\dfrac{1}{3}\); \(\dfrac{2}{3}\); \(\dfrac{4}{3}\)
TN
1
27 tháng 9 2021
Câu 5:
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
c: Xét tứ giác AEDF có
\(\widehat{EAF}=\widehat{AFD}=\widehat{AED}=90^0\)
Do đó: AEDF là hình chữ nhật
mà AD là tia phân giác của \(\widehat{FAE}\)
nên AEDF là hình vuông
28 tháng 10 2021
Kẻ đường cao AH
Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
Áp dụng HTL: \(BH=\dfrac{AB^2}{BC}=\dfrac{18}{5}\left(cm\right);AH=\dfrac{AB\cdot AC}{BC}=\dfrac{24}{5}\left(cm\right)\)
Vì AD là p/g nên \(\dfrac{BD}{DC}=\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow BD=\dfrac{3}{4}DC\)
Mà \(BD+DC=BC=10\Rightarrow\dfrac{7}{4}DC=10\Rightarrow DC=\dfrac{40}{7}\left(cm\right)\)
\(\Rightarrow BD=\dfrac{30}{7}\left(cm\right)\)
\(\Rightarrow HD=BD-BH=\dfrac{30}{7}-\dfrac{18}{5}=\dfrac{24}{35}\)
Áp dụng PTG: \(AD=\sqrt{AH^2+HD^2}=\sqrt{\left(\dfrac{24}{35}\right)^2+\left(\dfrac{24}{5}\right)^2}=\dfrac{24\sqrt{2}}{7}\approx4,85\left(cm\right)\)
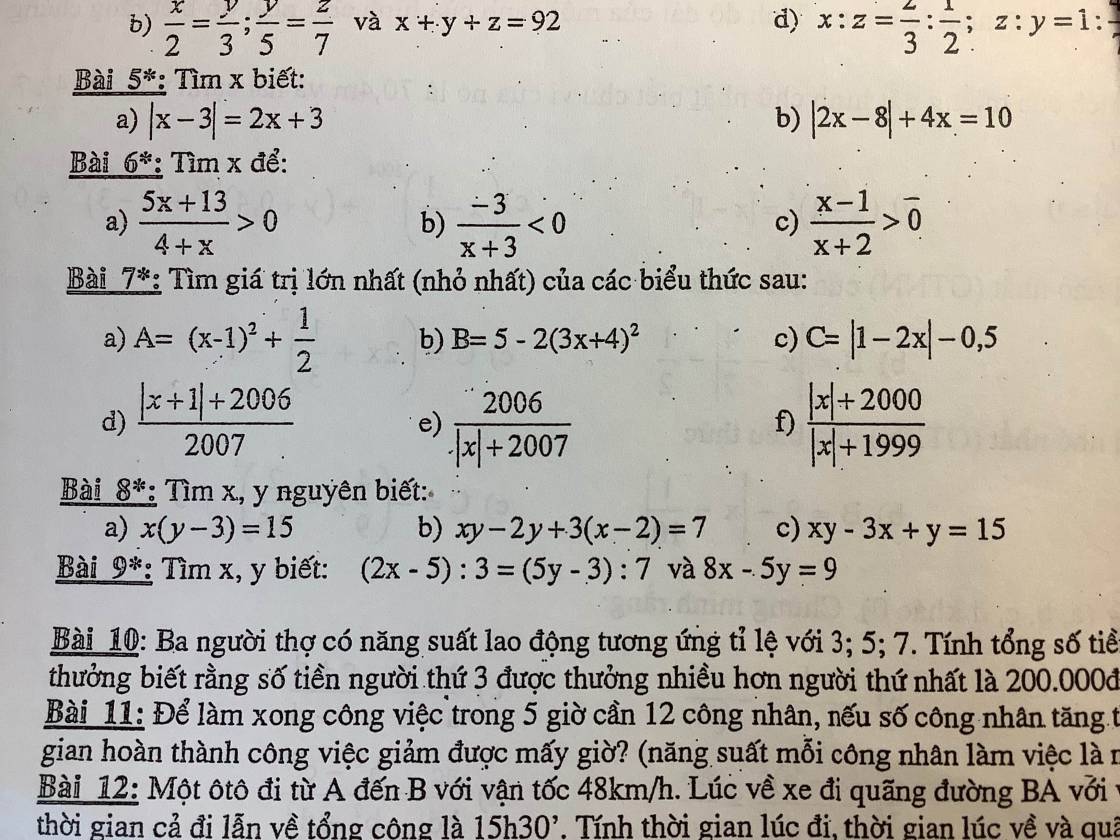
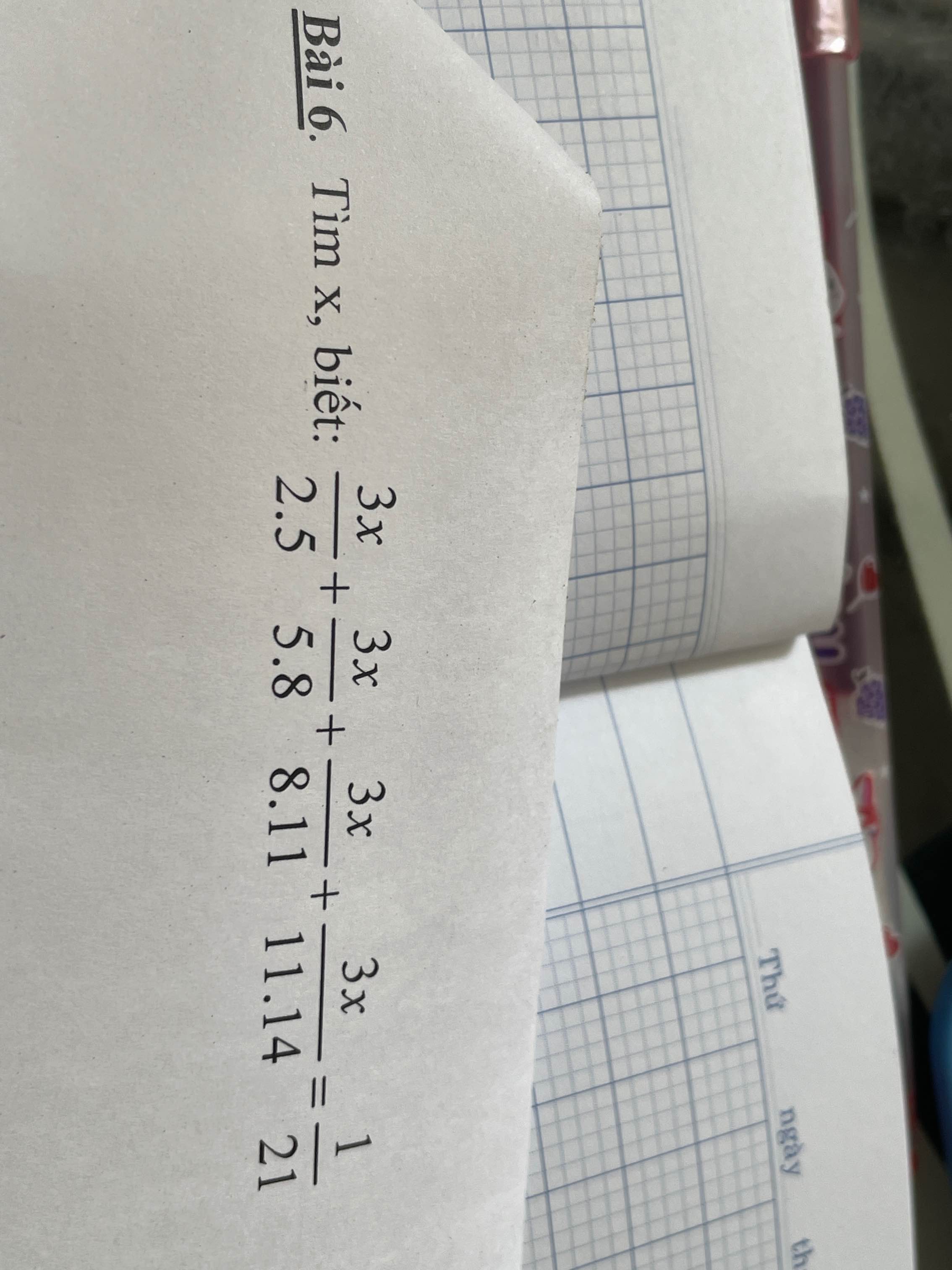
a) Nguyên tố A thuộc nhóm IIIA
=> A hóa trị III
CT muối sunfua của A là X2S3
CT muối bromua của nguyên tố A là ABr3
Ta có: \(\dfrac{M_{A_2S_3}}{M_{ABr_3}}=\dfrac{2A+32.3}{A+80.3}=\dfrac{50}{89}\)
=> A =27
Vậy nguyên tố A là Al
b) Hợp chất của Al với C : Al4C3
Al có hóa trị III, áp dụng quy tắc hóa trị => Hóa trị của C trong hợp chất là IV
Al có số oxh +3 => Số oxh của C là -4