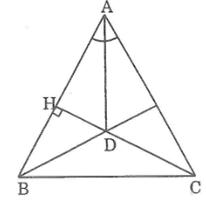
Cho tam giác ABC cân tại A (A không là góc vuông) có đường cao BH.Chứng minh...
Đọc tiếp
Cho tam giác ABC cân tại A (A không là góc vuông) có đường cao BH.Chứng minh :1/CH=2AB/BC2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 6 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
BD=CE
góc ABD=góc ACE
=>ΔADB=ΔAEC
=>AB=AC
=>ΔABC cân tại A
b: ΔABC cân tại A
mà AD là đường phân giác
nên AD vuông góc BC
Xét ΔABC có
AD,CH là đường cao
AD cắt CH tại D
=>D là trực tâm
=>BD vuông góc AC
11 tháng 2 2018
https://docs.google.com/document/d/1Wuo1vFdubrUg8F8-Ng_f-K8sda_JE_rRM704rtBrI-Q/edit?usp=sharing
Ta có H1+ H2+H3=180
E1+E2=180
mà E1=H1
nên E2=H2+H3
Tong 3 goc trong tam giác: E2+H2+A1=180
(H2+H3)+H2+A1=180
2.H2+H3+A1=180
SUY RA: H2=(180-90-A1):2 *** H3=90 hihi
=45-A1/2
mà A1=90-2A2
thay vào *** ta có H2=45-(90-2.A2)/2=A2
vậy H2=A2 hay EH//AD
31 tháng 8 2016
∞ Xét ▲ABK và ▲ACH có :
Góc A chung
Góc E = Góc D = 1v
AB = AC ( ▲ABC cân tại A )
Nên ▲ABK = ▲ACH (chgn) → AH = AK
∞ Xét ▲ADH và ▲ADK có :
AD chung
Góc H = Góc K = 1v
AH = AK (cmt)
Nên ▲ADH = ▲ADK (chcgv) → \(A_1=A_2\) kết hợp với AD nằm giữa AB và AC → AD phân giác góc A mà trong tam giác cân phân giác cũng là đường cao nên AD là đường cao hay BD _|_ AC.
CHÚC BẠN HỌC TỐT !!!
16 tháng 3 2022
a) \(\widehat{DAC}=\widehat{DAB}+\widehat{BAC}=\widehat{CAE}+\widehat{BAC}=\widehat{BAE}\)
\(AD=AB;AC=AE\)
\(\Rightarrow\)△ADC=△ABE (c-g-c).
b) AB cắt DC tại F.
\(90^0=\widehat{DAF}=180^0-\widehat{DFA}-\widehat{ADF}=180^0-\widehat{BFK}-\widehat{FBK}=\widehat{FKB}\)
\(DB^2+KC^2=DK^2+KB^2+BC^2-KB^2=BC^2+DK^2\)
16 tháng 3 2022
a) \(\widehat{DAC}=\widehat{DAB}+\widehat{BAC}=\widehat{CAE}+\widehat{BAC}=\widehat{BAE}\)
\(AD=AB;AC=AE\)
\(\Rightarrow\)△ADC=△ABE (c-g-c).
b) AB cắt DC tại F.
\(90^0=\widehat{DAF}=180^0-\widehat{DFA}-\widehat{ADF}=180^0-\widehat{BFK}-\widehat{FBK}=\widehat{FKB}\)
\(DB^2+KC^2=DK^2+KB^2+BC^2-KB^2=BC^2+DK^2\)
c) Trên tia đối IA lấy G sao cho IA=IG
\(\Rightarrow\)△ADI=△GEI (c-g-c) \(\Rightarrow\)AD//GE.
△DGI=△EAI (c-g-c) \(\Rightarrow\)DG//AE ; DG=AE=AC.
\(90^0+\widehat{BAH}+\widehat{DAG}+90^0+\widehat{GAE}+\widehat{HAC}=360^0\)
\(\Rightarrow\widehat{BAC}+\widehat{DAE}=180^0\)
\(\Rightarrow\widehat{BAC}=\widehat{ADG}\)
\(\Rightarrow\)△ADG=△BAC (c-g-c).
\(\widehat{ABC}+\widehat{BAH}=\widehat{DAG}+\widehat{BAH}=90^0\)
KK
16 tháng 3 2022
Câu a)
Ta có : góc BAD = góc CAE ( = 90 độ )
=> góc BAD + góc BAC = góc CAE + góc BAC
=> góc DAC = góc BAE
Xét tam giác DAC và tam giác BAE có :
góc DAC = góc BAE ( CMT )
AD = AB ( do tam giác ABD vuông cân tại A )
AC = AE ( do tam giác ACE vuông cân tại A )
=> tam giác DAC = tam giác BAE ( cgc )
=> DC = BE ( cặp cạnh tương ứng )
và góc ADC = góc ABE ( cặp góc tương ứng )
Gọi DC giao BE tại H
Gọi DC giao AB tại O
Do tam giác ADO vuông tại A ( GT )
=> góc ODA + góc DOA = 90 độ
Mà góc ODA = góc ABH ( CMT )
và góc DOA = BOH ( 2 góc đối đỉnh )
=> góc BOH + góc OHB = 90 độ
=> tam giác OBH vuông tại H
=> OH vuông góc BH
hay DC vuông góc BE
Vậy....