K
Khách
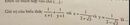
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
25 tháng 6 2016
Tóm tắt :
C : 8 cm
TT : ... cm3?
Công thức :
V = a x a x a
Thể tích ru bích là :
8 x 8 x 8 = 512 ( cm3)
Đáp số : 512 cm3.
H
5
9 tháng 7 2019
\(x^2+5x+1=\left(x+5\right)\sqrt{x^2+1}\)
<=> \(\left(x+5\right)\left(x-\sqrt{x^2+1}\right)=-1\)
Nhân liên hợp ta có
\(x+5=x+\sqrt{x^2+1}\)
=> \(x^2+1=25\)
=> \(x=\pm2\sqrt{6}\)
Vậy \(x=\pm2\sqrt{6}\)
26 tháng 7 2023
Câu 1: Đoạn trích trên được viết theo thể thơ tự do.
Câu 2: Phép liệt kê được sử dụng trong khổ thơ thứ nhất của đoạn trích được phép liệt kê không đồng nhất, khi liệt kê hai hành động của mẹ: "vẫn luôn ở đây" và "ôm con".
Câu 3: Hai dòng thơ "Mẹ sinh ra con giống như thân cây này sân bóng chiếc lá có gốc rụng lo vun trồng" có nội dung nhấn mạnh sự quan tâm, chăm sóc và tình thương của mẹ dành cho con. Mẹ đã sinh ra con và chăm sóc con như một cây trồng, lo vun trồng để con có thể phát triển và trưởng thành.
Câu 4: Trong cuộc sống, việc trẻ tìm cách từ chối ân cần của cha mẹ có thể được thông cảm. Đôi khi, trẻ em có thể cảm thấy áp lực từ sự quan tâm quá mức của cha mẹ, và muốn có không gian riêng để tự phát triển và khám phá bản thân. Tuy nhiên, việc từ chối ân cần của cha mẹ cần được xem xét kỹ lưỡng, và nhân đôi khi cần có sự đồng ý và hiểu biết giữa cha mẹ và con để đảm bảo mối quan hệ gia đình tốt đẹp.
ND
3
10 tháng 3 2016
Thời gian Hương đến sớm hơn giờ hẹn là:
10 giờ 40 phút -10 giờ 20 phút=20 phút
Thời gian Hương phải đợi Hồng là:
20 phút +15 phút= 35 phút
Đáp số: 35 phút
H
19 tháng 7 2021
a)
$n_{Nito} = \dfrac{6,02.10^{23}}{6,02.10^{23}} = 1(mol)$
$m_{Nito} = 1.14 = 14(gam)$
b)
$n_{Cl} = \dfrac{6,02.10^{23}}{6,02.10^{23}} = 1(mol)$
$m_{Cl} = 1.35,5 = 35,5(gam)$
c)
$n_{H_2O} = \dfrac{6,02.10^{23}}{6,02.10^{23}} = 1(mol)$
$m_{H_2O} = 1.18 = 18(gam)$
TP
19 tháng 7 2021
a) \(n_{N_2}=\dfrac{6,02.10^{23}}{6,02.10^{23}}=1\left(mol\right)\)
=> \(m_{N_2}=1.28=28\left(g\right)\)
b) \(n_{Cl_2}=\dfrac{6,02.10^{23}}{6,02.10^{23}}=1\left(mol\right)\)
=> \(m_{Cl_2}=1.35,5.2=71\left(g\right)\)
c) \(n_{H_2O}=\dfrac{6,02.10^{23}}{6,02.10^{23}}=1\left(mol\right)\)
=> \(m_{H_2O}=1.18=18\left(g\right)\)
d) \(n_{CaCO_3}=\dfrac{6,02.10^{23}}{6,02.10^{23}}=1\left(mol\right)\)
=> \(m_{CaCO_3}=1.100=100\left(g\right)\)
NK
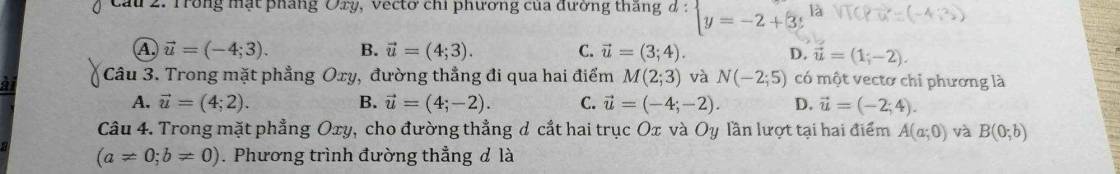giúp mình câu 3 với nha, giải ra luôn ạ
1
ĐK: \(x\ne-1;y\ne-1\)
Ta có: \(x=\frac{1}{2+\sqrt{3}}=\frac{2-\sqrt{3}}{4-3}=2-\sqrt{3}\left(tm\right)\)
\(y=\frac{1}{2-\sqrt{3}}=\frac{2+\sqrt{3}}{4-3}=2+\sqrt{3}\left(tm\right)\)
Thay \(x=2-\sqrt{3};y=2+\sqrt{3}\) vào biểu thức ta có:
\(\frac{1}{2-\sqrt{3}+1}+\frac{1}{2+\sqrt{3}+1}=\frac{1}{3-\sqrt{3}}+\frac{1}{3+\sqrt{3}}=\frac{3+\sqrt{3}+3-\sqrt{3}}{9-3}=\frac{6}{6}=1\)
Vậy ....
\(\frac{1}{x+1}+\frac{1}{y+1}=\frac{1}{\frac{1}{2+\sqrt{3}}+1}+\frac{1}{\frac{1}{2-\sqrt{3}}+1}\)
\(=\frac{1}{\frac{1+2+\sqrt{3}}{2+\sqrt{3}}}+\frac{1}{\frac{1+2-\sqrt{3}}{2-\sqrt{3}}}\)
\(=\frac{2+\sqrt{3}}{3+\sqrt{3}}+\frac{2-\sqrt{3}}{3-\sqrt{3}}\)
\(=\frac{\left(2+\sqrt{3}\right)\left(\sqrt{3}-1\right)+\left(2-\sqrt{3}\right)\left(\sqrt{3}+1\right)}{\sqrt{3}\left(\sqrt{3}+1\right)\left(\sqrt{3}-1\right)}\)
\(=\frac{2\sqrt{3}}{2\sqrt{3}}=1\)