chứng minh rằng: n4+6.n3+11.n2+6n chia hết cho 24
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
1
PT
1
CM
7 tháng 11 2017
A = n 4 – 2 n 3 – n 2 +2n = (n – 2)(n – 1)n(n + 1) là tích của 4 số nguyên liên tiếp do đó A ⋮ 24 .
CM
10 tháng 5 2017
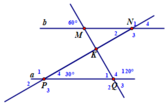
a. Q ^ 1 = 60 ° ( kề bù với Q ^ 4 ) mà Q 1 ^ đồng vị với M ^ = 60 ° => a//b
b. Vì a//b N 4 ^ = P ^ 4 = 30 ° ( đồng vị) ⇒ N ^ 1 = N ^ 3 = 150 ° ⇒ N ^ 4 = N ^ 2 = 130 °
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 9 2021
a.
Đề bài sai, ví dụ \(n=1\) lẻ nhưng \(1^2+4.1+8=13\) ko chia hết cho 8
b.
n lẻ \(\Rightarrow n=2k+1\)
\(n^3+3n^2-n-3=n^2\left(n+3\right)-\left(n+3\right)=\left(n^2-1\right)\left(n+3\right)=\left(n-1\right)\left(n+1\right)\left(n+3\right)\)
\(=\left(2k+1-1\right)\left(2k+1+1\right)\left(2k+1+3\right)\)
\(=8k\left(k+1\right)\left(k+2\right)\)
Do \(k\left(k+1\right)\left(k+2\right)\) là tích 3 số tự nhiên liên tiếp nên chia hết cho 6
\(\Rightarrow8k\left(k+1\right)\left(k+2\right)\) chia hết cho 48
CM
7 tháng 2 2018
Rút gọn được n 3 – n. Biến đổi thành Q = n(n – 1)(n + 1). Ba số nguyên liên tiếp trong đó sẽ có 1 số chia hết cho 2 và 1 số chia hết cho 3, vì Q ⋮ 6.
TP
1
KV
5 tháng 1
Ta có:
n(n + 1)(n + 2)
= (n² + n)(n + 2)
= n³ + 2n² + n² + 2n
= n³ + 3n² + 2n
Mà n(n + 1)(n + 2) là tích của ba số nguyên liên tiếp (do n là số nguyên)
⇒ n(n + 1)(n + 2) ⋮ 3
⇒ (n³ + 3n² + 2) ⋮ 3
Ta có:
n³ + 11n
= n³ + 3n² + 2n - 3n² + 9n
= (n³ + 3n² + 2n) - 3n(n - 3)
Ta có:
3 ⋮ 3
⇒ 3n(n - 3) ⋮ 3 (với mọi n nguyên)
Mà (n³ + 3n² + 2n) ⋮ 3 (cmt)
⇒ [(n³ + 3n² + 2n) - 3n(n - 3)] ⋮ 3
Vậy (n³ + 11n) ⋮ 3 với mọi số nguyên n
26 tháng 10 2022
Vì đây là 7 số nguyên liên tiếp
nên A chia hết cho 7!
=>A chia hết cho 5040
4 tháng 10 2021
Bài 2:
\(n^3-n^2+2n+7⋮n^2+1\)
\(\Leftrightarrow n^3+n-n^2-1+n+8⋮n^2+1\)
\(\Leftrightarrow n^2-64⋮n^2+1\)
\(\Leftrightarrow n^2+1\in\left\{1;65\right\}\)
\(\Leftrightarrow n\in\left\{0;8;-8\right\}\)
S
2
KV
15 tháng 10 2018
Ta có
A =n[n2(n2 -7)2 -36]= n[(n3 -7n2)-36]
= n(n3 -7n2 -6)( n3 -7n2 +6)
Mà n3 -7n2 -6 = (n+1) (n+2) (n-3)
n3 -7n2 +6 = (n-1)(n-2)(n+3)
Do đó:
A= (n-3)(n-2)(n-1)(n+1)(n+2)(n+3)
Đây là tích của 7 số nguyên liên tiếp.Trong 7 số nguyên liên tiếp
+Tồn tại một bội của 5 ⇒ A chia hết cho 5
+Tồn tại một bội của 7 ⇒ A chia hết cho 7
+Tồn tại hai bội của 3 ⇒ A chia hết cho 9
+Tồn tại ba bội số của 2,trong đó có một bội số của 4 ⇒ A chia hết cho 16
A chia hết cho các số 5,7,9,16 đôi một nguyên tố cùng nhau nên A chia hết cho
5.7.9.16 =5040.
+ Qua ví dụ 1 rút ra cách làm như sau:
Gọi A(n) là một biểu thức phụ thuộc vào n (n ∈ N hoặc n ∈ Z).
HM
1 tháng 6 2021
n^3-n^2+2n+7=(n^3+n)-(n^2+1)+n+8=n(n^2+1)-(n^2+1)+n+8. Để n(n^2+1)-(n^2+1)+n+8 chia hết cho n^2+1=>8+n chia hết cho n^2+1
Vậy n=2k hoặc 2k+1
Xét TH:n=2k
=>8+n=8+2k(1)
*n^2+1=(2k)^2+1=4k^2+1(2)
Từ (1) và (2) ta có:8+2k chia hết cho 2 mà 4k^2+1 không chia hết cho 2 nên n ko bằng 2k
Xét TH:n=2k+1=>8+n=8+2k+1(3)
*n^2+1=(2k+1)^2+1
n^2+1=(4k^2+1)+(2k+1)(4)
Từ 3 và 4 : muốn 8+n chia hết n^2 +1 thì 8 chia hết cho 4k^2+1
=>4k^2+1 thuộc{-1;+1;-2;+2;-4;+4;-8;8}
các bạn làm từng TH thì sẽ ra k=0 và n=1 và các bạn thế vào đề bài lai để kiểm tra kết quả
n4+6n3+11n2+6n
=(n4+5n3+6n2)+(n3+5n2+6n)
=(n2+n)(n2+5n+6)
=n(n+1)(n2+3n+2n+6)
=n(n+1)(n+2)(n+3)
Do n ; n+1;n+2;n+3 là 4 số nguyên liên tiếp nên tồn tại 1 số chia hết cho 2 , 1 số chia hết cho 3,1 số chia hết cho 4
=>n(n+1)(n+2)(n+3) chia hết cho 2.3.4=24(đpcm)