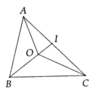
\(\text{Cho điểm O nằm trong }\)\(\Delta ABC\). \(\text{Chứng minh rằng: }\)\(\frac{AB+BC+CA}{2}< OA+OB+OC< AB+BC+CA\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: OA + OB + OC = OA + OB + OC = (OA + OB) + OC = AB + OC < AB + BC + CA (vì OC < BC) Vậy ta có: OA + OB + OC < AB + BC + CA (1) Ta cũng có: OA + OB + OC = OA + OB + OC = (OA + OC) + OB = AC + OB < AB + BC + CA (vì OB < AB) Vậy ta có: OA + OB + OC < AB + BC + CA (2) Từ (1) và (2), ta có: OA + OB + OC < AB + BC + CA Tương tự, ta có: OA + OB + OC = OA + OB + OC = (OB + OC) + OA = BC + OA > 0A + OB + OC (vì BC > 0A) Vậy ta có: OA + OB + OC > 0A + OB + OC (3) Ta cũng có: OA + OB + OC = OA + OB + OC = (OA + OB) + OC = AB + OC > 0A + OB + OC (vì AB > 0A) Vậy ta có: OA + OB + OC > 0A + OB + OC (4) Từ (3) và (4), ta có: OA + OB + OC > 0A + OB + OC Vậy ta có: 0A + OB + OC < AB + BC + CA < OA + OB + OC

Ta có:
\(OA+OB< AC+BC\)
\(OA+OC< AB+BC\)
\(OC+OB< AB+AC\)
Cộng theo từng vế ba bất đẳng thức trên ta được :
\(2\left(OA+OB+OC\right)< 2\left(AB+AC+BC\right)\)
hay \(OA+OB+OC< AB+AC+BC\)(1)
Mặt khác trong các tam giác OAB,OBC,OCA,theo bất đẳng thức tam giác ta lại có :
\(OA+OB>AB\)
\(OB+OC>BC\)
\(OC+OA>AC\)
Cộng theo từng vế ba bất đẳng thức trên, ta được :
\(2\left(OA+OB+OC\right)>AB+BC+AC\)
hay \(OA+OB+OC>\frac{AB+AC+BC}{2}\)(2)
Từ (1) và (2) :
\(\Rightarrow\frac{AB+AC+BC}{2}< OA+OB+OC< AB+AC+BC.\)


 tham khảo nha
tham khảo nha
Gọi M là giao của OA và BC
Xét tam giác ABM có
AM < AB + BM
=> OA + OM < AB + BM (1)
Xét tam giác OCM có:
OC < OM + CM (2)
Từ (1) và (2) =>
=> OA + OM + OC < AB + BM + OM + CM
=> OA + OC < AB + BC (3)
Chứng minh tương tự:
OA + OB < AC + BC (4)
OB + OC < AB + AC (5)
Từ (3), (4) và (5) => 2OA + 2OB + 2OC < 2AB + 2BC + 2AC
=> OA + OB + OC < AB + BC + CA (*)
Xét tam giác OAB có:
AB < OA + OB (6)
Tương tự: AC < OA + OC (7)
BC < OB + OC (8)
Từ (6), (7), (8) => AB + BC + CA < 2OA + 2OB + 2OC
=> \(\frac{AB+BC+CA}{2}< OA+OB+OC\) (**)
Từ (*) và (**)
\(\Rightarrow\frac{AB+BC+CA}{2}< OA+OB+OC< AB+BC+CA\)
hình bạn tự vẽ nha!
vì góc COB lớn hơn góc CBO suy ra cạnh CB>BO (1)
vì góc BOA >góc OAB suy ra cạnh AB>AO(2)
vì góc AOC>góc OCA suy ra cạnh AC>OC (3)
từ (1),(2),(3) suy ra OA+OB+OC<AB+BC+CA
còn chứng minh AB+BC+CA /2<OA+OB+OC mình suy nghĩ đã nha