Bài 2 giúp mik vs
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Phương trình hoành độ giao điểm:
\(x^2=2\left(m-1\right)x-m+2\Leftrightarrow x^2-2\left(m-1\right)x+m-2=0\) (1)
a.
(d) cắt (P) tại 2 điểm nằm về 2 phía trục tung khi và chỉ khi (1) có 2 nghiệm pb trái dấu
\(\Leftrightarrow ac=m-2< 0\)
\(\Rightarrow m< 2\)
b.
Xét (1), ta có \(\Delta'=\left(m-1\right)^2-\left(m-2\right)=m^2-3m+3=\left(m-\dfrac{3}{2}\right)^2+\dfrac{3}{4}>0;\forall m\)
\(\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m
Hay (d) luôn cắt (P) tại 2 điểm pb với mọi m

\(\left|2x-3\right|=3-2x\)
\(ĐK:x\le\dfrac{3}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=3-2x\\3-2x=3-2x\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\0=0\left(đúng\right)\end{matrix}\right.\)
Vậy \(S=\left\{x\in R;x=\dfrac{3}{2}\right\}\)


\(2,\\ a,=\sqrt{\dfrac{8a\left(5-a\right)^2}{a-5}}=\sqrt{\dfrac{8a\left(a-5\right)^2}{a-5}}=\sqrt{8a\left(a-5\right)}=2\sqrt{2a\left(a-5\right)}\\ b,=\sqrt{\dfrac{\left(x-7\right)^2\left(x+7\right)}{\left(7-x\right)\left(7+x\right)}}=\sqrt{\dfrac{\left(7-x\right)^2\left(x+7\right)}{\left(7-x\right)\left(7+x\right)}}=\sqrt{7-x}\\ c,=\sqrt{\dfrac{a^2b}{b^2a}}=\sqrt{\dfrac{a}{b}}=\dfrac{\sqrt{ab}}{b}\\ d,=\sqrt{\dfrac{6x^2}{x}}=\sqrt{6x}\)

2:
2.1:
a: P(x) chia hết cho 2x+3
=>6x^3+9x^2-16x^2-24x+8x+12+m-12 chia hết cho 2x+3
=>m-12=0
=>m=12
b: P(x)=6x^3-7x^2-16x+12
P(x)/(3x-2)
\(=\dfrac{6x^3-4x^2-3x^2+2x-18x+12}{3x-2}=2x^2-x-6\)
Số dư là 0
2.2:
Tham khảo:
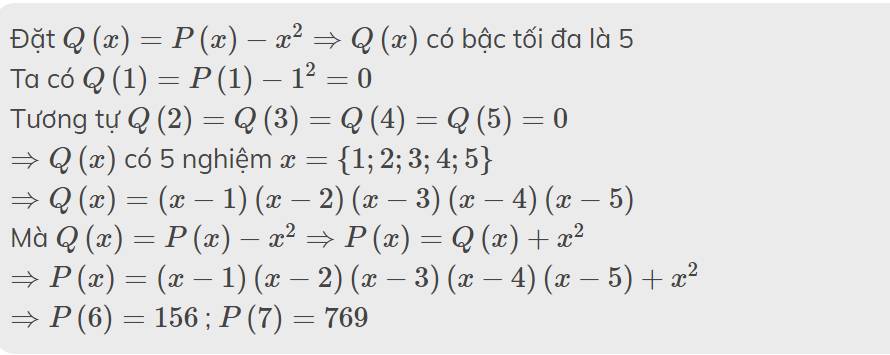

Bài 2: CTHH của câu d là Na3PO4
Bài 4:
| Na | Ca | Fe(II) | Fe(III) | Al | |
| Cl(I) | NaCl 58,5 | CaCl2 111 | FeCl2 127 | FeCl3 162,5 | AlCl3 133,5 |
| SO4 (II) | Na2SO4 142 | CaSO4 136 | FeSO4 152 | Fe2(SO4)3 400 | Al2(SO4)3 342 |
| PO4 (III) | Na3PO4 164 | Ca3(PO4)2 310 | Fe3(PO4)2 358 | FePO4 151 | AlPO4 122 |
| OH (I) | NaOH 40 | Ca(OH)2 74 | Fe(OH)2 90 | Fe(OH)3 107 | Al(OH)3 78 |







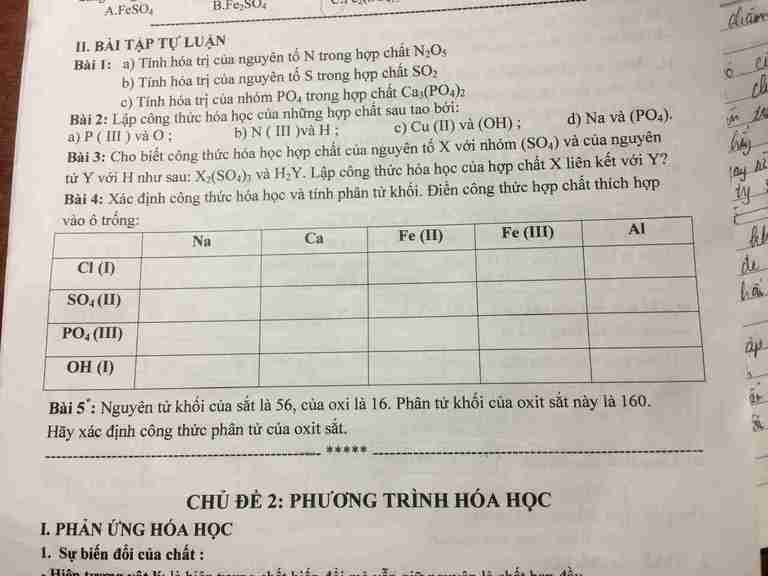






Bài 2 :
a, - Thay hoành độ của A và B vào hàm số ta được :
\(\left\{{}\begin{matrix}y_A=1\\y_B=4\end{matrix}\right.\)
Vậy \(A\left(-2;1\right),B\left(4;4\right)\)
b, - Gọi phương trình đường thẳng AB có dạng \(y=ax+b\)
- Thay tọa độ của A và B vào ta được :
\(\left\{{}\begin{matrix}-2a+b=1\\4a+b=4\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=2\end{matrix}\right.\)
Vậy phương trình đường thẳng AB là : \(y=\dfrac{1}{2}x+2\)