Mik đang cần gấp giúp mik giải vs ạ! Mik cảm ơn ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
14 tháng 10 2021
bạn tự vẽ hình giúp mik nha
a.ta có \(\Delta\)ABC nội tiếp (O) và AB là đường kính nên \(\Delta\)ABC vuông tại C
trong \(\Delta ABC\) vuông tại C có
AC=AB.cosBAC=10.cos30=8,7
BC=AB.sinCAB=10.sin30=5
ta có Bx là tiếp tuyến của (O) nên Bx vuông góc với AB tại B
trong \(\Delta\)ABE vuông tại B có
\(cosBAE=\dfrac{AB}{AE}\Rightarrow AE=\dfrac{AB}{cosBAE}=\dfrac{10}{cos30}=11,5\)
mà:CE=AE-AC=11,5-8,7=2,8
b.áp dụng pytago vào \(\Delta ABE\) vuông tại B có
\(BE=\sqrt{AE^2-AB^2}=\sqrt{11,5^2-10^2}=5,7\)
25 tháng 9 2021
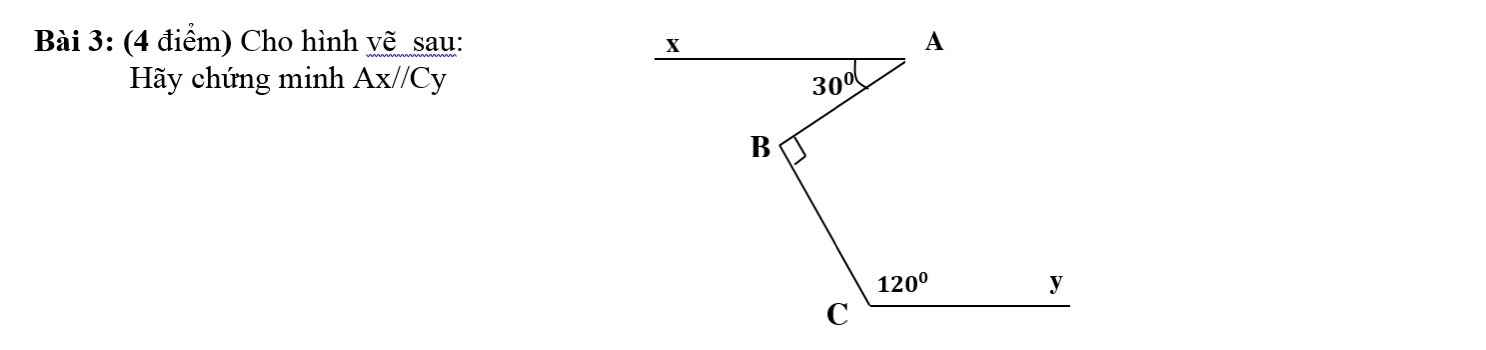
Kẻ Bz//Ax
Ta có: Ax//Bz
\(\Rightarrow\widehat{BAx}=\widehat{ABz}=30^0\)(so le trong)
\(\Rightarrow\widehat{zBC}=\widehat{ABC}-\widehat{BAx}=90^0-30^0=60^0\)
Ta có: \(\widehat{zBC}+\widehat{BCy}=60^0+120^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> Bz//Cy
Mà Bz//Ax
=> Ax//Cy
TC
1
13 tháng 7 2023
2:
a: |x-2021|=x-2021
=>x-2021>=0
=>x>=2021
b: 5^x+5^x+2=650
=>5^x+5^x*25=650
=>5^x*26=650
=>5^x=25
=>x=2
c: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{2x+3y-2-6}{2\cdot2+3\cdot3}=2\)
=>x-1=4 và y-2=6
=>x=5 và y=8
5:
a: Xét tứ giác ABKC có
M là trung điểm chung của AK và BC
=>ABKC là hình bình hành
=>góc ABK=180 độ-góc CAB=80 độ
b: ABKC là hình bình hành
=>góc ABK=góc ACK
góc DAE=360 độ-góc CAB-góc BAD-góc CAE
=180 độ-góc CAB=góc ACK
Xét ΔABK và ΔDAE có
AB=DA
góc ABK=góc DAE
BK=AE
=>ΔABK=ΔDAE
24 tháng 1 2023
a: Xét (O) có
EM,EA là tiếp tuyến
nên EM=EA và OE là phân giác của góc MOA(1)
Xét (O) có
FM,FB là tiếp tuyến
nên FM=FB và OF là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc FOE=1/2*180=90 độ
b: EF=EM+MF
=>EF=EA+FB
c: Xét ΔOEF vuông tại O có OM là đường cao
=>ME*MF=OM^2
=>ME*MF=OA^2
9 tháng 1 2022
Bài 2:
a: Xét ΔABC có
X là trung điểm của BC
Y là trung điểm của AB
Do đó: XY là đường trung bình
=>XY//AC và XY=AC/2=3,5(cm)
hay XZ//AC và XZ=AC
b: Xét tứ giác AZBX có
Y là trung điểm của AB
Y là trung điểm của ZX
Do đó: AZBX là hình bình hành
mà \(\widehat{AXB}=90^0\)
nên AZBX là hình chữ nhật
d: Xét tứ giác AZXC có
XZ//AC
XZ=AC
Do đó: AZXC là hình bình hành
BA
1
21 tháng 7 2023
4*cos(pi/6-a)*sin(pi/3-a)
=4*(cospi/6*cosa+sinpi/6*sina)*(sinpi/3*cosa-sina*cospi/3)
=4*(căn 3/2*cosa+1/2*sina)*(căn 3/2*cosa-1/2*sina)
=4*(3/4*cos^2a-1/4*sin^2a)
=3cos^2a-sin^2a
=3(1-sin^2a)-sin^2a
=3-4sin^2a
=>m=3; n=-4
m^2-n^2=-7
BA
1
20 tháng 7 2023
Ta có:
\(\dfrac{1}{cos^2x-sin^2x}+\dfrac{2tanx}{1-tan^2x}=\dfrac{1}{cos2x}+tan2x=\dfrac{1}{cos2x}+\dfrac{sin2x}{cos2x}=\dfrac{1+sin2x}{cos2x}=\dfrac{cos2x}{1-sin2x}\)
\(\Rightarrow P=a+b=2+1=3\)
13 tháng 12 2021
\(a,\dfrac{11x}{2x-5}+\dfrac{x-30}{2x-5}=\dfrac{11x+x-30}{2x-5}=\dfrac{12x-30}{2x-5}=\dfrac{6\left(2x-5\right)}{2x-5}=6\)
\(b,\dfrac{3x^2-1}{2x}+\dfrac{x^2+1}{2x}=\dfrac{3x^2-1+x^2+1}{2x}=\dfrac{4x^2}{2x}=2x\)
\(c,\dfrac{3}{2x-5}+\dfrac{-2}{2x+5}+\dfrac{-20}{4x^2-25}=\dfrac{3\left(2x+5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{2\left(2x-5\right)}{\left(2x-5\right)\left(2x+5\right)}-\dfrac{20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{6x+15-4x+10-20}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{2x+5}{\left(2x-5\right)\left(2x+5\right)}=\dfrac{1}{2x-5}\)
\(d,\dfrac{x-2}{x-1}+\dfrac{x-3}{x+1}+\dfrac{4-2x^2}{x^2-1}=\dfrac{\left(x-2\right)\left(x+1\right)+\left(x-3\right)\left(x-1\right)+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2-2x+x-2+x^2-3x-x+3+4-2x^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5x+5}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{-5}{x-1}\)
\(e,\dfrac{x+1}{x-1}+\dfrac{1-x}{x+1}+\dfrac{4}{x^2-1}=\dfrac{\left(x+1\right)^2}{\left(x-1\right)\left(x+1\right)}-\dfrac{\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}+\dfrac{4}{\left(x-1\right)\left(x+1\right)}=\dfrac{x^2+2x+1-x^2+2x-1+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4x+4}{\left(x-1\right)\left(x+1\right)}=\dfrac{4\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{4}{x-1}\)
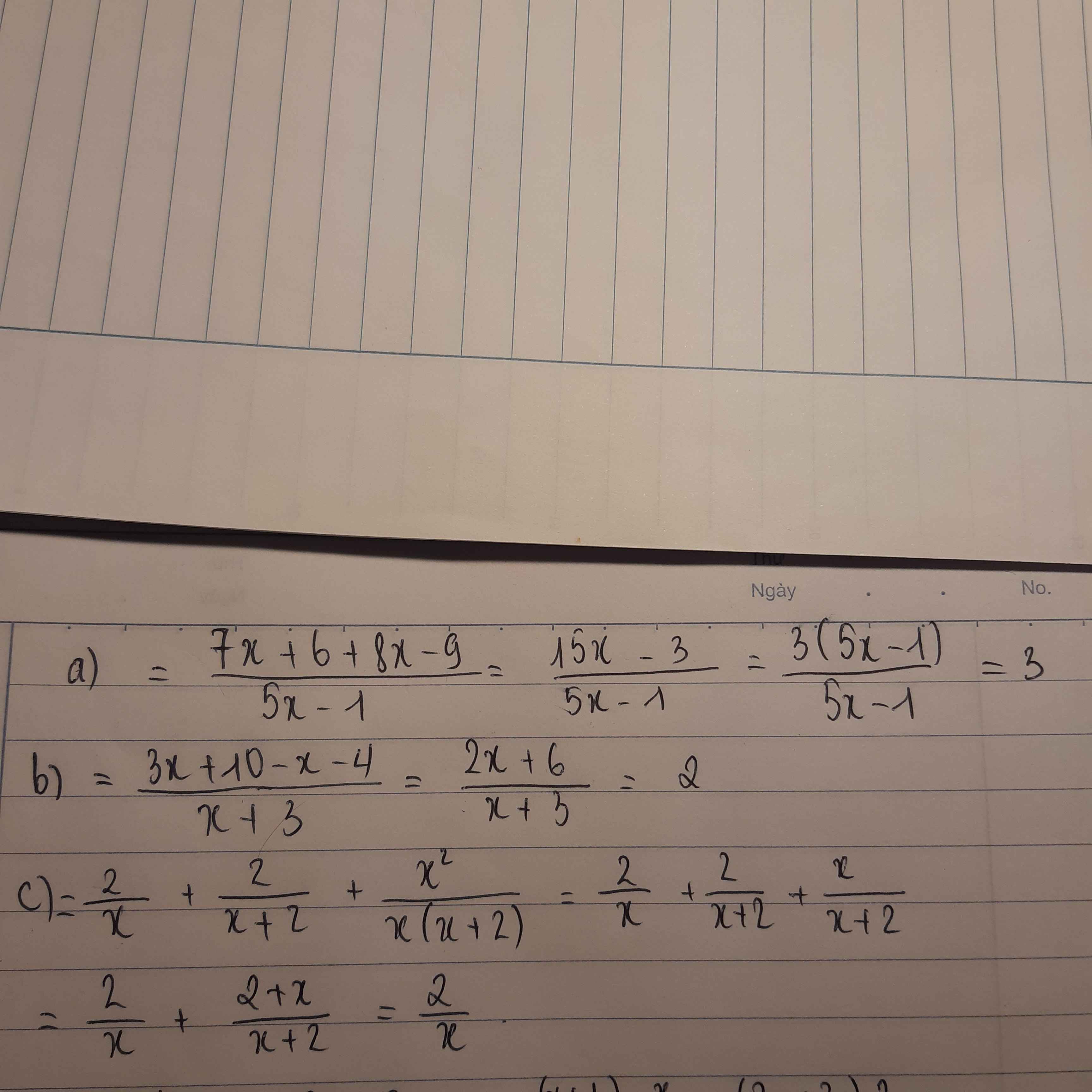
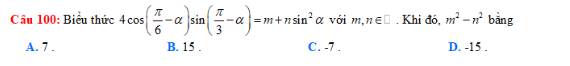
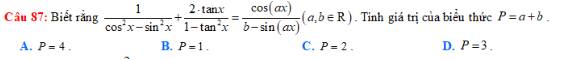
1 are
2 am
3 is
4 are
5 are
6 are
7 is
8 is
9 is
10 are
IV
1 is writing
2 are losing
3 is having
4 is staying
5 am not lying
6 is always using
7 are having
8 Are you playing
9 are not touching
10 Is - listening
11 Is- winning
12 am not staying
13 is not working
14 is not reading
15 isn't raining
16 am not listening
17 Are they making
18 Are you doing
19 Is - sitting
20 is - doing
21 are-putting
22 are-wearing
23 is-studying
2, am
3, is
4,are
5,are
6,are
7,is
8,is
9,is
10,are
IV
1,2,7 OK
3,is having
4,has stayed
5,am not lying
6,always uses
8,Are-playing
9,not to touch
10,Is-listening
11,Are-winning
12,am not staying
13,isn't working
14,isn't reading
15,isn't raining
16,am not listening
17,Are-making
18,Are-doing
19,Is-sitting
20,is-doing
21,do-putting
22,do-wear
23,is-studying