Tổng sau có chia hết cho 3 không? Vì sao?
a) A = 1012 + 1 b) 1012 + 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HV
28 tháng 8 2021
a,ko chia hết cho 9,3
b,chia hết cho 9,3
c,chia hết cho 9,3
d,chia hết cho 3 ko chia hết cho 9
tick mik nha
PT
1
CM
3 tháng 1 2019
1012 – 1 =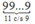 
Tổng các chữ số bằng 9 + 9 + … + 9 = 99 chia hết cho 3 và 9
Do đó 1012 – 1 chia hết cho cả 3 và 9.
H9
HT.Phong (9A5)
CTVHS
21 tháng 10 2023
Bài 4:
a chia 11 dư 5 dạng tổng quát của a là:
\(a=11k+5\left(k\in N\right)\)
b chia 11 dư 6 dạng tổng quát của b là:
\(b=11k+6\left(k\in N\right)\)
Nên: \(a+b\)
\(=11k+5+11k+6\)
\(=\left(11k+11k\right)+\left(5+6\right)\)
\(=k\cdot\left(11+11\right)+11\)
\(=22k+11\)
\(=11\cdot\left(2k+1\right)\)
Mà: \(11\cdot\left(2k+1\right)\) ⋮ 11
\(\Rightarrow a+b\) ⋮ 11
H9
HT.Phong (9A5)
CTVHS
21 tháng 10 2023
Bài 1: Mình làm rồi nhé !
Bài 2:
a) Dạng tổng quát của A là:
\(a=36k+24\left(k\in N\right)\)
b) a chia hết cho 6 vì:
Ta có: \(36k\) ⋮ 6 và 24 ⋮ 6
\(\Rightarrow a=36k+24\) ⋮ 6
c) a không chia hết cho 9 vì:
Ta có: \(36k\) ⋮ 9 và 24 không chia hết cho 9
\(\Rightarrow a=36k+24\) không chia hết cho 9
NQ
1
12 tháng 12 2015
ta thấy : \(2^2\) chia hết cho \(2^2\)
\(2^3\)chia hết cho \(2^2\)
....
\(2^{2012}\)chia hết cho \(2^2\)
=> \(2^2+2^3+...+2^{2012}\) chia hết cho \(2^2\)
mà 2 ko chia hết cho \(2^2\)
=> S ko chia hết cho 4 hay S ko phải là số CP
VN
1
H9
HT.Phong (9A5)
CTVHS
24 tháng 2 2023
a. \(10^{12}+1=1000000000001\) không chia hết cho 3 và 9 suy ra \(10^{12}+1\) không chia hết cho 3 và 9
1 tháng 10 2021
a) \(\left\{{}\begin{matrix}2.3.4.5.6⋮2\\82⋮2\end{matrix}\right.\)\(\Rightarrow2.3.4.5.6+82⋮2\)
\(\left\{{}\begin{matrix}2.3.4.5.6⋮5\\82⋮̸5\end{matrix}\right.\)\(\Rightarrow2.3.4.5.6+82⋮̸5\)
b) \(\left\{{}\begin{matrix}2.3.4.5.6⋮2\\95⋮̸2\end{matrix}\right.\)\(\Rightarrow2.3.4.5.6-95⋮̸2\)
\(\left\{{}\begin{matrix}2.3.4.5.6⋮5\\95⋮5\end{matrix}\right.\)\(\Rightarrow2.3.4.5.6-95⋮5\)
a) A = 1012 + 1
=> A = 100.......0 + 1
↼-------⇀
12 c/s 0
=> A = 100..........01
↼-------⇀
11 c/s 0
Tổng các chữ số của A là ;
1 + 0 . 11 + 1 = 2 ⁒ 3
=> A ⁒ 3
b) 1012 + 2
Làm tương tự như trên
=> Tổng các chữ số của giá trị của tổng trên là :
1 + 0 . 11 + 2 = 3 ⋮ 3
=> 1012 + 2 ⋮ 3