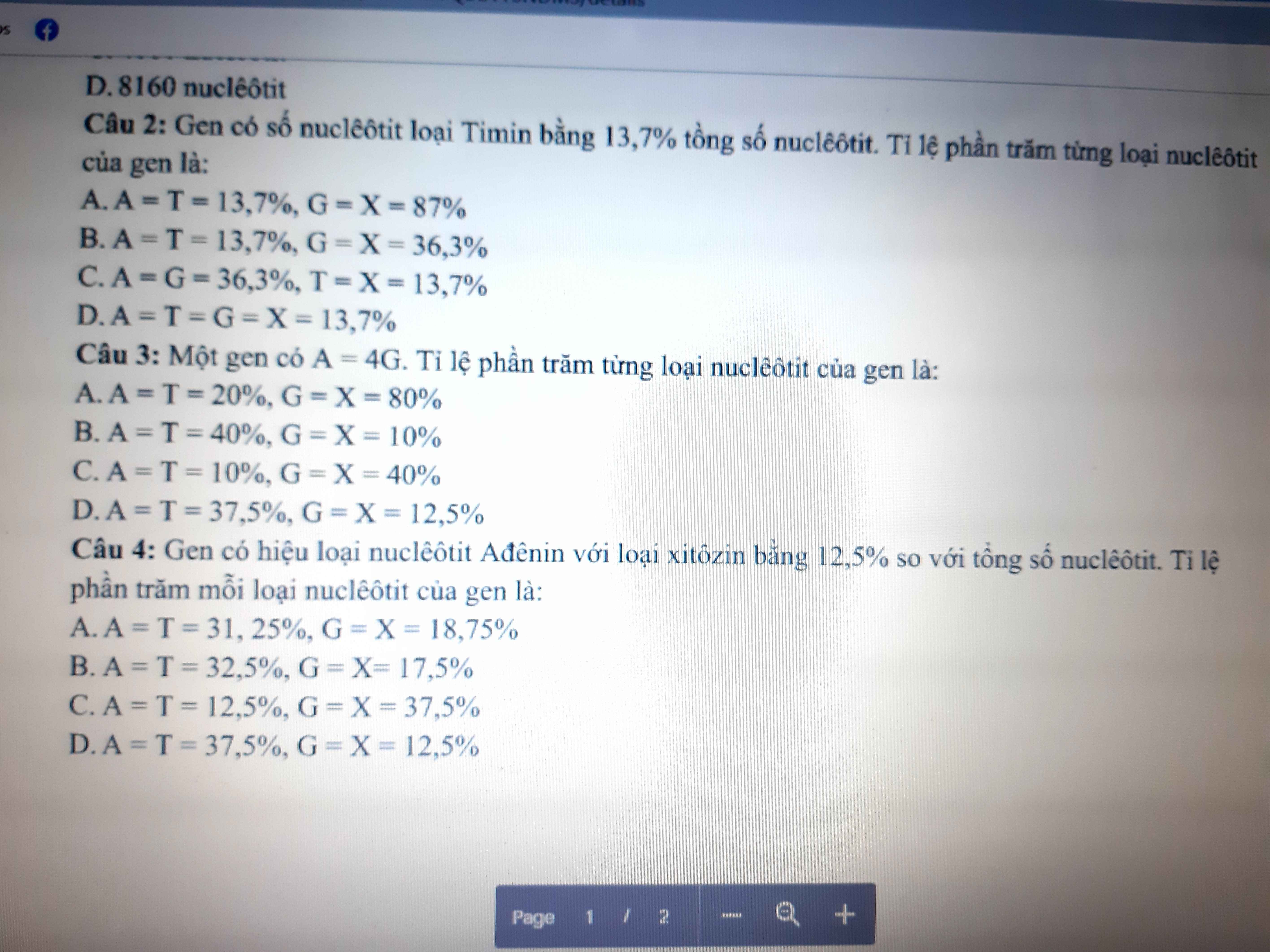
Giải rõ ra với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 2 2022
Câu 2.
Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot m\cdot6^2+m\cdot10\cdot0=18m\left(J\right)\)
a)Cơ năng tại nơi có độ cao cực đại:
\(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\Rightarrow h_{max}=\dfrac{18}{10}=1,8m\)
b)Cơ năng tại nơi \(W_t=W_đ\):
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\Rightarrow z=\dfrac{18}{2g}=\dfrac{18}{2\cdot10}=0,9m\)
c)Cơ năng tại nơi \(W_đ=2W_t\):
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{18}{3\cdot10}=0,6m\)
NM
1
A
22 tháng 6 2021
Ps : Bn tự vẽ hình nhé, mk chỉ giải thôi ạ.
a) Xét \(\Delta ABC\)và \(\Delta HAB\)
\(\widehat{BAC}=\widehat{BHA}=90^O\)
\(\widehat{ABC}chung\)
\(\Rightarrow\Delta ABC~\Delta HBA\)( g - g )
b) Xét \(\Delta AHD\)và \(\Delta CED\)
\(\widehat{AHD}=\widehat{CED}=90^O\)
\(\widehat{ADH}=\widehat{CDE}\)( đối đỉnh )
\(\Rightarrow\Delta AHD~\Delta CED\left(g-g\right)\)
\(\Rightarrow\frac{AH}{AD}=\frac{CE}{CD}\Rightarrow AH.CD=AD.CE\)
c) Vì H là trung điểm của BD mà \(AH\perp BD\)
=> AH là đường trung trực của BD
\(\Rightarrow AB=AD\)
Mà : \(\frac{AH}{AD}=\frac{CE}{CD}\)
\(\Rightarrow\frac{AH}{AB}=\frac{CE}{CD}\)
Vì \(\Delta ABC~\Delta HBA\Rightarrow\frac{AH}{AB}=\frac{CA}{CB}\)
Do đó : \(\frac{CE}{CD}=\frac{CA}{CB}=\frac{8}{10}=\frac{4}{5}\)
Vì \(\Delta CED\)vuông
\(\Rightarrow S_{CED}=\frac{CE.ED}{2}\)
\(AB//FK\Rightarrow\widehat{BAH}=\widehat{KFH}\)
\(\widehat{AHB}=\widehat{FHK}=90^O\)
\(BA=HD\)
\(\Rightarrow\Delta AHB=\Delta FHK\)
\(\Rightarrow HA=HF\)mà \(CH\perp AF\)
=> CH là đường trung trực AF \(\Rightarrow\Delta ACF\)cân tại C
Do đó : D là trọng tâm \(\Delta ACF\)
\(\Rightarrow CD=\frac{2}{3}CH\)
Mà \(\cos ACB=\frac{AC}{BC}=\frac{CH}{CA}=\frac{4}{5}\Rightarrow CH=\frac{32}{5}\Rightarrow CD=\frac{64}{15}\)
\(\Rightarrow\frac{CE}{CD}=\frac{4}{5}\Rightarrow CE=\frac{256}{75}\)
\(ED=\sqrt{CD^2-CE^2}=\frac{64}{25}\)
\(\Rightarrow S_{CED}=\frac{8192}{1875}\)
d) Vì \(\Delta ACF\)cân tại C \(\Rightarrow KE//AF\Rightarrow\widehat{EKF}=\widehat{AFK}\)
Vì HK là trung tuyến \(\Delta AFK\)\(\Rightarrow\widehat{AFK}=\widehat{HKF}\)
Do đó : \(\widehat{HKF}=\widehat{EKF}\)
=> KD là phân giác \(\widehat{HKE}\)
# Aeri #
HV
0
C1
4
KM
30 tháng 7 2017
Giải :
3x + 1 = 2x + 10
=> 3x - 2x = 10 - 1
=> x = 9
Bài này ta áp dụng quy tắc chuyển vế đổi dấu ở lớp 6 nha bạn !!
30 tháng 7 2017
3x + 1 = 2x + 10 <=> 2x +x + 1 = 2x + 10
<=> x + 1 = 10
<=> x = 10 - 1 = 9
Vậy x thỏa mãn là : x = 9
C1
1
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2022
Pt bậc 2 có 2 nghiệm trái dấu khi \(ac< 0\)
\(\Leftrightarrow\left(m^2-4\right)m< 0\)
\(\Leftrightarrow m\in\left(-\infty;-2\right)\cup\left(0;2\right)\)
DT
1
S
13 tháng 1 2022
Câu 2 : B (vik T + X luôn = 50% nên lấy 50% - T -> X và G)
Câu 3 : B (vik A + G = 50% mak A = 4G thik thay vào lak tính đc A vs G)
Câu 4 : A (vik A - X = 12.5% mak A + X = 50%,giải hệ lak tìm đc A vs X)
25 tháng 2 2022
Bài 2.
Tóm tắt:
\(v=6\)m/s, \(g=10\)m/s2
a)\(h_{max}=?\)
b)\(W_t=W_đ\Rightarrow z=?\)
c)\(W_đ=2W_t\Rightarrow z'=?\)
Giải chi tiết:
Cơ năng tại vị trí ban đầu:
\(W=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot m\cdot6^2=18m\left(J\right)\)
a)Tại nơi có độ cao \(h_{max}\): \(W_1=mgh_{max}\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow18m=mgh_{max}\)
\(\Rightarrow h_{max}=\dfrac{18}{g}=\dfrac{18}{10}=1,8m\)
b)Tại nơi thế năng bằng động năng thì cơ năng là
\(W_2=W_đ+W_t=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow18m=2mgz\)
\(\Rightarrow z=\dfrac{18}{2g}=\dfrac{9}{10}=0,9m\)
c)Tại nơi động năng bằng hai lần thế năng:
\(W_3=W_đ+W_t=3W_t=3mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow18m=3mgz'\)
\(\Rightarrow z'=\dfrac{18}{3g}=\dfrac{6}{10}=0,6m\)
25 tháng 2 2022
Bài 3.
a)Cơ năng ban đầu: \(W=W_đ+W_t\)
\(\Rightarrow W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}m\cdot0^2+m\cdot10\cdot20=200m\left(J\right)\)
Cơ năng tại nơi vận tốc vật khi cham đất:
\(W'=\dfrac{1}{2}mv'^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow200m=\dfrac{1}{2}mv'^2\)
\(\Rightarrow v'=20\)m/s
Cách khác nè:Áp dụng công thức( chỉ sử dụng khi tính vận tôc vật chạm đất)
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot20}=20\)m/s
b)Tại nơi có thế năng bằng động năng thì cơ năng là:
\(W_1=W_t+W_đ=2W_t=2mgh\)
Bảo toàn cơ năng: \(W_1=W\)
\(\Rightarrow2mgh=200m\)
\(\Rightarrow h=10m\)
c)Cơ năng tại nơi thế năng gấp 3 động năng:
\(W_2=W_đ+W_t=W_đ+3W_đ=4W_đ=4\cdot\dfrac{1}{2}mv'^2=2mv'^2\)
Bảo toàn cơ năng: \(W_2=W\)
\(\Rightarrow200m=2mv'^2\)
\(\Rightarrow v'=10\)m/s
27 tháng 2 2022
Cơ năng tại vị trí ban đầu:
\(W=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot m\cdot8^2=32m\left(J\right)\)
a)Cơ năng tại nơi có độ cao cực đại:
\(W_1=mgh_{max}\left(J\right)\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow32m=mgh_{max}\Rightarrow h_{max}=\dfrac{32}{g}=\dfrac{32}{10}=3,2m\)
b)Cơ năng tại nơi \(W_t=W_đ\):
\(W_2=2W_t=2mgz\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow32m=2mgz\Rightarrow z=\dfrac{32}{2g}=\dfrac{32}{2\cdot10}=1,6m\)
c)Cơ năng tại nơi \(W_t=\dfrac{1}{4}W_đ\Rightarrow W_đ=4W_t\):
\(W_3=5W_t=5mgz'\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow32m=5mgz'\Rightarrow z'=\dfrac{32}{5g}=\dfrac{32}{5\cdot10}=0,64m\)
