Giải giúp mình bài 4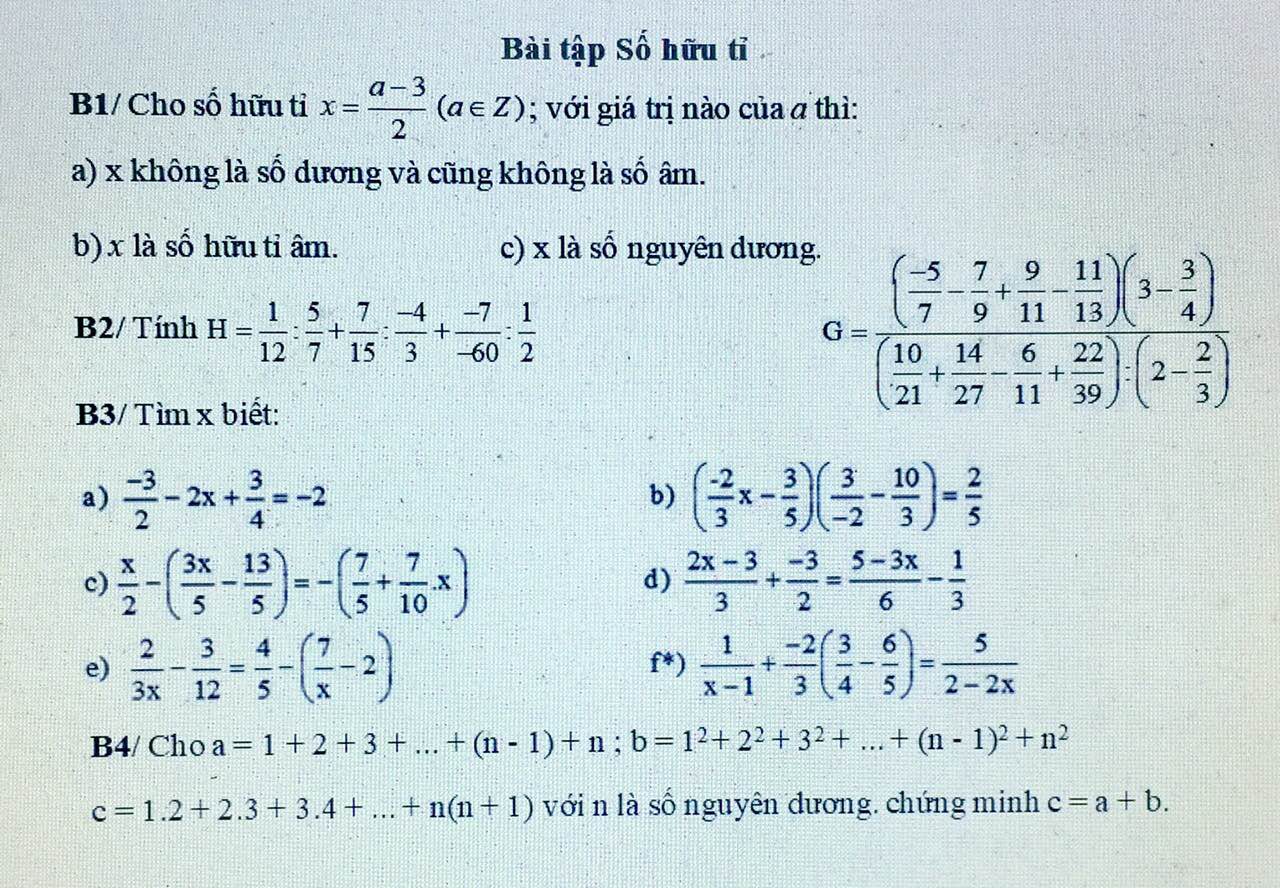
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
YH
0
3T
1
18 tháng 6 2023
4:
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
góc BAC=90 độ
=>ABDC là hcn
=>ΔACD vuông tại C
b: Xét ΔKAB vuông tại A và ΔKCD vuông tại C có
KA=KC
AB=CD
=>ΔKAB=ΔKCD
=>KB=KD
c: Xét ΔACD có
DK,CM là trung tuyến
DK cắt CM tại I
=>I là trọng tâm
=>KI=1/3KD
Xét ΔCAB có
AM,BK là trung tuyến
AM cắt BK tại N
=>N là trọng tâm
=>KN=1/3KB=KI
YH
0
26 tháng 5 2023
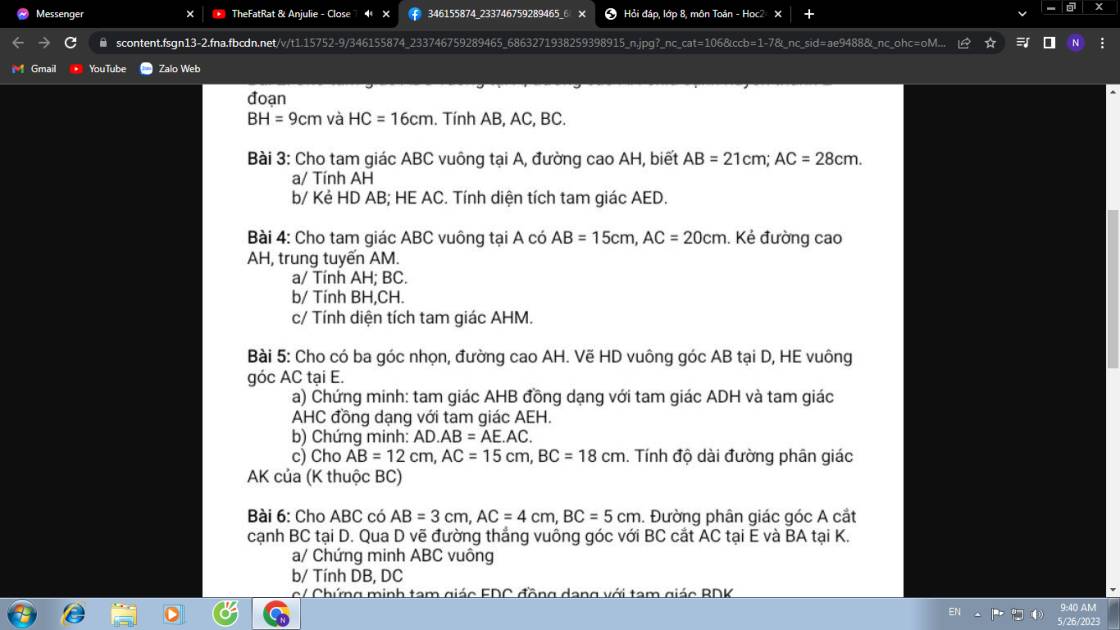
4:
a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
b: BH=15^2/25=9cm
CH=25-9=16cm
c: AM=25/2=12,5cm
HM=căn 12,5^2-12^2=3,5cm
S AHM=1/2*3,5*12=6*3,5=21cm2
NH
0
9 tháng 4 2021
a, 0 < a < \(\dfrac{\pi}{2}\) tức a là góc nhọn
⇒ sinA = \(\sqrt{1-\dfrac{16}{13^2}}=\dfrac{3\sqrt{17}}{13}\)
tan = sin/cos
cot = cos/sin (cái này tự tính nhá)
b, \(\dfrac{3\pi}{2}< a< 2\pi\) ⇔ \(270^0< a< 360^0\)
⇒ sin(a) < 0
cos (a) > 0
cot = - 3 => tan = \(\dfrac{-1}{3}\)
\(\dfrac{sin}{cos}=\dfrac{-1}{3}\), mà sin^2 + cos^2 = 1
sin < 0; cos >0
⇒ \(\left\{{}\begin{matrix}sin=-\dfrac{\sqrt{10}}{10}\\cos=\dfrac{3\sqrt{10}}{10}\end{matrix}\right.\)
14 tháng 6 2023
4:
2:
Δ=(2m-1)^2-4(m+3)
=4m^2-4m+1-4m-12
=4m^2-8m-11
Để pt có 2 nghiệm thì 4m^2-8m-11>=0
=>m<=(2-căn 15)/2 hoặc m>=(2+căn 15)/2
x1+x2=2m-1 và 2x1+3x2=13
=>2x1+2x2=4m-2 và 2x1+3x2=13
=>-x2=4m-15 và x1+x2=2m-1
=>x2=-4m+15 và x1=2m-1+4m-15=6m-16
x1x2=m+3
=>-24m^2+64m+90m-240=m+3
=>m=27/8 hoặc m=3
Bài 4:
Số số hạng của dãy A là:
n-1+1=n(số)
Tổng của dãy A là:
\(a=\dfrac{\left(n+1\right)\cdot n}{2}\)
Ta có: \(b=1^2+2^2+3^2+...+\left(n-1\right)^2+n^2\)
\(=1+2\left(1+1\right)+3\left(2+1\right)+...+n\left(n-1+1\right)\)
\(=\dfrac{n\left(n+1\right)}{2}+\dfrac{n\left(n+1\right)\left(n-1\right)}{3}\)
\(=\dfrac{3n\left(n+1\right)}{6}+\dfrac{2n\left(n+1\right)\left(n-1\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\)
Ta có: \(c=1\cdot2+2\cdot3+3\cdot4+...+n\left(n+1\right)\)
\(\Leftrightarrow3c=1\cdot2\cdot3+2\cdot3\cdot4+3\cdot4\cdot3+...+3n\left(n+1\right)\)
\(\Leftrightarrow3c=n\left(n+1\right)\left(n+2\right)\)
\(\Leftrightarrow c=\dfrac{n\left(n+1\right)\left(n+2\right)}{3}\)
Ta có: \(a+b=\dfrac{\left(n+1\right)n}{2}+\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}\)
\(=\dfrac{3n\left(n+1\right)+n\left(n+1\right)\left(2n+1\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(3+2n+1\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(2n+4\right)}{6}\)
\(=\dfrac{n\left(n+1\right)\left(n+2\right)}{3}\)
=c(đpcm)