K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
19 tháng 1 2022
a. \(y\text{×}\dfrac{1}{5}-\dfrac{2}{3}=\dfrac{1}{4}\)
\(y\text{×}\dfrac{1}{5}=\dfrac{1}{4}+\dfrac{2}{3}\)
\(y=\dfrac{11}{12}:\dfrac{1}{5}=\dfrac{55}{12}\)
b. \(\dfrac{8}{5}-y:\dfrac{1}{2}=1\)
\(y:\dfrac{1}{2}=\dfrac{8}{5}-1\)
\(y=\dfrac{6}{5}\)
c. \(y\text{×}\dfrac{3}{4}+y\text{×}\dfrac{1}{4}-y=99\)
\(y\text{×}\left(\dfrac{3}{4}+\dfrac{1}{4}-1\right)=99\)
\(y\text{×}0=99\) (vô lí)
=> Không có giá trị y nào thỏa mãn.
d. \(\dfrac{y}{2}+\dfrac{y}{3}+\dfrac{y}{6}=1\)
\(\dfrac{3\text{×}y+2\text{×}y+y}{6}=\dfrac{6}{6}\)
\(\Rightarrow3\text{×}y+2\text{×}y+y=6\)
\(y\text{×}\left(3+2+1\right)=6\) hay \(y\text{×}6=6\)
\(y=1\)
e. \(\dfrac{y}{2}-\dfrac{7}{3}=\dfrac{1}{6}\)
\(\dfrac{y}{2}=\dfrac{1}{6}+\dfrac{7}{3}=\dfrac{5}{2}\)
\(y=5\)
f. \(\dfrac{15}{y-2}=\dfrac{3}{7}\)
\(\dfrac{15}{y-2}=\dfrac{15}{35}\) \(\Rightarrow y-2=35\)
\(y=37\)
Các bài g, h còn lại bạn làm tương tự như bài f.
20 tháng 8 2019
a) Ta có:
f(0) = -2.03 + 3.02 - 0 + 5 = 0 + 0 - 0 + 5 = 5
g(-1) = 2.(-1)3 - 2.(-1)2 + (-1) - 9 = -2 - 2 - 1 - 9 = -14
b) f(x) + g(x) = (-2x3 + 3x2 - x + 5) + (2x3 - 2x2 + x - 9)
= -2x3 + 3x2 - x + 5 + 2x3 - 2x2 + x - 9
= (-2x3 + 2x3) + (3x2 - 2x2) - (x - x) + (5 - 9)
= x2 - 4
f(x) - g(x) = (-2x3 + 3x2 - x + 5) - (2x3 - 2x2 + x - 9)
= -2x3 + 3x2 - x + 5 - 2x3 + 2x2 - x + 9
= -(2x3 + 2x3) + (3x2 + 2x2) - (x + x) + (5 + 9)
= -4x3 + 5x2 - 2x + 14
1 tháng 6 2019
Ta có : G(0) = a.02 + b.0 + c = 4
=> c = 4
G(1) = a.12 + b.1 + c = 9
=> a + b + c = 9
Mà c = 4 => a + b = 9 - 4 = 5 (1)
G(2) = a.22 + b.2 + c = 14
=> 4a + 2b + c = 14
Mà c = 4 > 4a + 2b = 14 - 4 = 10 => 2a + b = 5 (2)
Từ (1) và (2) trừ vế cho vế :
(a + b) - (2a + b) = 5 - 5
=> -a = 0 => a = 0
Thay a = 0 vào (1), ta được : 0 + b = 5 => b = 5
Vậy ...
1 tháng 6 2019
\(G\left(0\right)=4\Rightarrow a.0^2+b.0+c=c=4\)
\(G\left(1\right)=9\Rightarrow a.1^2+b.1+c=a+b=9\)
\(G\left(2\right)=14\Rightarrow a.2^2+b.2+c=4a+2b=2.\left(2a+b\right)=14\)
\(\Rightarrow2a+b=7\)
Ta có: 2a + b - (a + b) = a = -2
=> b = 9 - (-2) = 11
Vậy a = -2; b = 11; c = 0
15 tháng 4 2018
ta có: f(x) + g(x) = ( 7 x^6 - 6x ^5 +5x^4 -4x^3 +3x^2 -2x +1) - ( x - 2x^2 +3x^3 - 4x^4 + 5x^5 - 6x^6)
\(=7x^6-6x^5+5x^4-4x^3+3x^2-2x+1-x+2x^2-3x^3+4x^4-5x^5+6x^6\)
\(=\left(7x^6+6x^6\right)-\left(6x^5+5x^5\right)+\left(5x^4+4x^4\right)-\left(4x^3+3x^3\right)+\left(3x^2+2x^2\right)-\left(2x+x\right)+1\)
\(=13x^6-11x^5+9x^4-7x^3+5x^2-3x+1\)
Chúc bn học tốt !!!!!!
TN
Tống Ngọc Châu
VIP
4 tháng 12 2021
Uhhhhhhhhhhhhhhhhhhhhhhhhhh😥😥😥😥😥😥😥😥😥😥😥????????????...............
7 tháng 5 2018
Cho f(x) = 0
=> ( x -2 ).( x+3) = 0
=> x -2 = 0 => x= 2
x + 3 = 0 => x = - 3
=> x =2 , x = -3 là nghiệm của f(x)
mà nghiệm của f(x) cũng là nghiệm của g(x)
=> x = 2; x = -3 là nghiệm của g(x)
ta có: x = 2 là nghiệm của g(x)
=> 2^3 + a. 2^2 + b. 2 + 2 = 0
8 + 4a + 2b + 2 = 0
2.( 4 + 2a + b + 1) =0
=> 4 + 2a + b + 1 = 0
2a + b + 5 = 0
b = -5 - 2a
ta có: x = -3 là nghiệm của g(x)
=> (-3)^3 + a . ( -3)^2 + b.(-3) + 2 = 0
- 27 + 9a - 3b + 2 = 0
- 25 + 9a - 3.( -5 - 2a) = 0
- 25 + 9a + 15 + 6a = 0
-10 + 15 a = 0
15a = 10
a = 10 / 15
a = 2/3
mà b = -5 - 2a
b = -5 - 2. 2/3
b = - 5 - 4/ 3
b = -19/3
KL: a = 2/3, b = -19/3
24 tháng 12 2018
Cho \(x=\frac{1}{4}\Rightarrow2.f\left(\frac{1}{\frac{1}{4}}\right)=\left(\frac{1}{4}\right)^2\)
\(\Rightarrow2f\left(4\right)=\frac{1}{16}\Rightarrow f\left(4\right)=\frac{1}{32}\)
XO
28 tháng 9 2020
Ta có f(k) = k3 + 2k2 + 15
= (k3 + 9k2 + 27k + 27) - (7k2 + 27k + 12)
= (k + 3)3 - (7k2 + 27k + 18) + 6
= (k + 3)3 - (7k2 + 21k + 6k + 18) + 6
= (k + 3)3 - [7k(k + 3) + 6(k + 3)] + 6
= (k + 3)3 - (7k + 6)(k + 3) + 6
= (k + 3)[(k + 3)2 - 7k - 6) + 6
Vì (k + 3)[(k + 3)2 - 7k - 6) \(⋮\)k + 3
=> f(k) \(⋮\)g(k) khi 6 \(⋮k+3\)
=> \(k+3\inƯ\left(6\right)\)(k là số tự nhiên)
=> \(k+3\in\left\{3;6\right\}\)(Vì k \(\ge\) 0 => k + 3 \(\ge\) 3)
=> \(k\in\left\{0;3\right\}\)
Vậy \(k\in\left\{0;3\right\}\)thì f(k) \(⋮\)g(k)
13 tháng 2 2016
Ta có quy luật :
\(\frac{1}{3}=\frac{1}{1.3}\)
\(\frac{1}{15}=\frac{1}{3.5}\)
\(\frac{1}{35}=\frac{1}{5.7}\)
........
\(\frac{1}{1599}=\frac{1}{39.41}\)
Vậy số thứ 20 của dãy số là : \(\frac{1}{1599}\)
10 tháng 5 2022
a: \(F\left(x\right)=x^3+2x^2+3x+4\)
\(G\left(x\right)=x^3-x^2+3x+1\)
b: \(F\left(x\right)+G\left(x\right)=2x^3+x^2+6x+5\)
\(F\left(x\right)-G\left(x\right)=3x^2+3\)
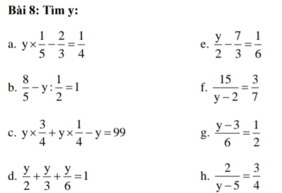
Trả lời:
f) \(x^2-2\sqrt{5}x+5=0\)
\(\Leftrightarrow x^2-2.x.\sqrt{5}+\left(\sqrt{5}\right)^2=0\)
\(\Leftrightarrow\left(x-\sqrt{5}\right)^2=0\)
\(\Leftrightarrow x-\sqrt{5}=0\)
\(\Leftrightarrow x=\sqrt{5}\)
câu f mình trả lời sai ạ