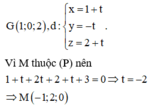Cho M = {x ∈ Z | -3 ≤ x < 2}. Ta có:A. 0 ⊂ MB. -3 ∉ MC. {-2; -1; 0} ⊂ MD. {-1; 0; 1} ⊂...
Đọc tiếp
Cho M = {x ∈ Z | -3 ≤ x < 2}. Ta có:
A. 0 ⊂ M
B. -3 ∉ M
C. {-2; -1; 0} ⊂ M
D. {-1; 0; 1} ⊂ M
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
VD
0
Những câu hỏi liên quan
30 tháng 1
Xét ΔMAC có \(\widehat{BMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{BMC}=\widehat{MAC}+\widehat{MCA}=60^0+\widehat{MCA}\)
=>\(\widehat{BMC}>60^0\)(1)
Vì M nằm giữa A và B
nên tia CM nằm giữa hai tia CA và CB
=>\(\widehat{ACM}+\widehat{BCM}=\widehat{ACB}\)
=>\(\widehat{BCM}+\widehat{ACM}=60^0\)
=>\(\widehat{BCM}< 60^0\left(2\right)\)
mà \(\widehat{B}=60^0\)(ΔABC đều)(3)
nên từ (1),(2),(3) suy ra \(\widehat{BMC}>\widehat{B}>\widehat{MCB}\)
=>BC>MC>MB
=>Chọn D
CM
12 tháng 5 2017
Chọn C
Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
TT
1
2 tháng 4 2022
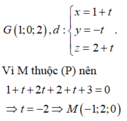
\(x=3-2\sqrt{2}=\sqrt{2^2}-2.1.\sqrt{2}+1^2=\left(\sqrt{2}-1\right)^2\)
\(A=\dfrac{\sqrt{\left(\sqrt{2}-1\right)^2}-4}{\sqrt{\left(\sqrt{2}-1\right)^2-2}}=\dfrac{\sqrt{2}-1-4}{\sqrt{2}-1-2}=\dfrac{\sqrt{2}-5}{\sqrt{2}-3}\)
3 tháng 4 2022
Viết bình phương chưa đúng
\(x=3-2\sqrt{2}=2+2\sqrt{2}+1=\left(\sqrt{2}\right)^2+2.\sqrt{2}.1+1^2=\left(\sqrt{2}+1\right)^2\)
ko nên viết bình vào căn nhé :)
CM
10 tháng 1 2017
Đáp án D.
Gọi I là điểm thỏa mãn
Ta có:
=> M là hình chiếu của I trên (P) dễ thấy
CM
13 tháng 2 2018
Đáp án C
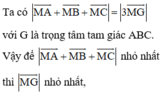
hay M là hình chiếu của G lên mặt phẳng (P).
Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
