Tại sao cos2 x =1/2 cos2x?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(A=cos^2x+\dfrac{1+cos\left(\dfrac{2\pi}{3}+2x\right)}{2}+\dfrac{1+cos\left(\dfrac{2\pi}{3}-2x\right)}{2}\\ =cos^2x+1+\dfrac{cos\left(\dfrac{2\pi}{3}+2x\right)+cos\left(\dfrac{2\pi}{3}-2x\right)}{2}\\ =cos^2x+1+cos\left(\dfrac{2\pi}{3}\right).cos2x\\ =cos^2x+1-\dfrac{1}{2}.cos2x=\dfrac{1+cos2x}{2}+1-\dfrac{cos2x}{2}=\dfrac{3}{2}.\)

cos2(x + kπ) = cos(2x + k2π) = cos2x, k ∈ Z.
Vậy hàm số y = cos 2x là hàm số chẵn, tuần hoàn, có chu kì là π.
Đồ thị hàm số y = cos2x
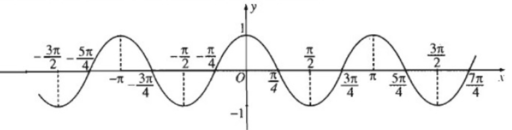
Đồ thị hàm số y = |cos2x|
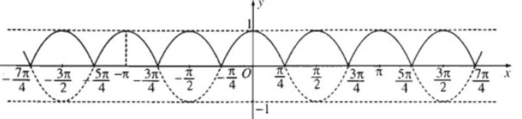

Chọn A.
Ta có: A= cos2( x-a) + cos2x -2cos a.cos x.cos( a - x).
= cos( x - a) [ cos(x - a) – 2cosa. cosx] + cos2x
= cos( x - a) [ cos x.cosa + sina.sinx – 2cosa.cosx] + cos2x
= cos( x - a) [ -cos x.cosa + sina.sinx] + cos2x
= -cos( x - a) .cos( x + a) + cos2x


Chọn C
ĐK: cos x ≠ 0
Khi đó, phương trình ![]()
![]()
![]()
![]() ( vì cos x
≠
0)
( vì cos x
≠
0)
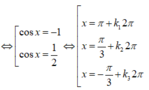
Vì ![]()
![]()
Áp dụng công thức tính tổng 11 số hạng đầu tiên của một cấp số cộng, ta có
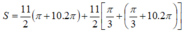

(Lưu ý: Tất cả các nghiệm này không có nghiệm nào trùng nhau. Và giả như phương trình có một số họ nghiệm trùng nhau thì tổng các nghiệm trên đoạn [1; 70] vẫn không thay đổi vì đề không yêu cầu tính tổng các nghiệm phân biệt ).

1.
ĐKXĐ: \(x\ne k\pi\)
\(\Leftrightarrow\left(2cos2x-1\right)\left(sinx-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos2x=\dfrac{1}{2}\\sinx=3>1\left(ktm\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\pi}{3}+k2\pi\\2x=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=-\dfrac{\pi}{6}+k\pi\end{matrix}\right.\)
2. Bạn kiểm tra lại đề, pt này về cơ bản ko giải được.
3.
ĐKXĐ: \(x\ne\dfrac{k\pi}{2}\)
\(\dfrac{3\left(sinx+\dfrac{sinx}{cosx}\right)}{\dfrac{sinx}{cosx}-sinx}-2cosx=2\)
\(\Leftrightarrow\dfrac{3\left(1+cosx\right)}{1-cosx}+2\left(1+cosx\right)=0\)
\(\Leftrightarrow\left(1+cosx\right)\left(\dfrac{3}{1-cosx}+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=-1\left(loại\right)\\cosx=\dfrac{5}{2}\left(loại\right)\end{matrix}\right.\)
Vậy pt đã cho vô nghiệm

a: \(\sqrt{3^2+2^2}=\sqrt{13}\)
Chia hai vế cho căn 13, ta được:
\(\dfrac{3}{\sqrt{13}}\cdot\sin2x+\dfrac{2}{\sqrt{13}}\cdot\cos2x=\dfrac{3}{\sqrt{13}}\)
Đặt \(\cos a=\dfrac{3}{\sqrt{13}}\)
Ta được phương trình: \(\sin\left(2x+a\right)=\cos a=\sin\left(\dfrac{\Pi}{2}-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+a=\dfrac{\Pi}{2}-a+k2\Pi\\2x+a=\dfrac{\Pi}{2}+a+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\left(\dfrac{\Pi}{2}-2a+k2\Pi\right)\\x=\dfrac{\Pi}{4}+k\Pi\end{matrix}\right.\)
b: \(\Leftrightarrow cos^2x-sin^2x+cosx-sinx=0\)
\(\Leftrightarrow\left(cosx-sinx\right)\left(cosx+sinx+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos x=\cos\left(\dfrac{\Pi}{2}-x\right)\\\sin\left(x-\dfrac{\Pi}{4}\right)=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{2}-x+k2\Pi\\x=-\dfrac{\Pi}{2}+x+k2\Pi\\x-\dfrac{\Pi}{4}=-\dfrac{\Pi}{2}+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{4}+k\Pi\\x=-\dfrac{\Pi}{4}+k2\Pi\end{matrix}\right.\)

Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2
\(cos^2x=\dfrac{1}{2}cos2x+\dfrac{1}{2}\) mới đúng
Nó là công thức hạ bậc (có trong SGK đại số 10)