
giúp mình câu 2 và câu 3 gấp nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Sau trận bãoTN//, chân trời, ngấn bểCN// sạch như tấm kính lau hết mây hết bụi. Mặt trời nhú lên dần dần, rồi lên cho kì hết.VN
b, Quả trứngCN// hồng hào thăm thẳm và đường bệ đặt lên một mâm bạc đường kính mâm rộng bằng cả một cái chân trời màu ngọc trai nước biển hửng hồng.VN
c, Mặt trờiCN// nhú lên dần dầnVN1,// rồi lên cho kì hếtVN2

3. Đoạn thơ nói về cảm giác thư thái, bình yên của người chiến sĩ khi dừng chân nghỉ ngơi và nghe tiếng gà nhảy ổ và những kỉ niệm tuổi thơ bỗng ùa về.

Tham khảo !
Cảm ơn thần Mặt Trời đã ban cho con hương thơm và sắc đẹp. Con hứa sẽ làm cho cuộc đời đẹp đẽ hơn.
#hoctot

Sorry nãy máy load chậm
\(\frac{-101}{-100}=\frac{101}{100}>1\)
\(\frac{200}{201}< 1\)
\(\Rightarrow\frac{200}{201}< \frac{101}{100}\Rightarrow\frac{200}{201}< \frac{-101}{-100}\)

Bài 4:
b: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
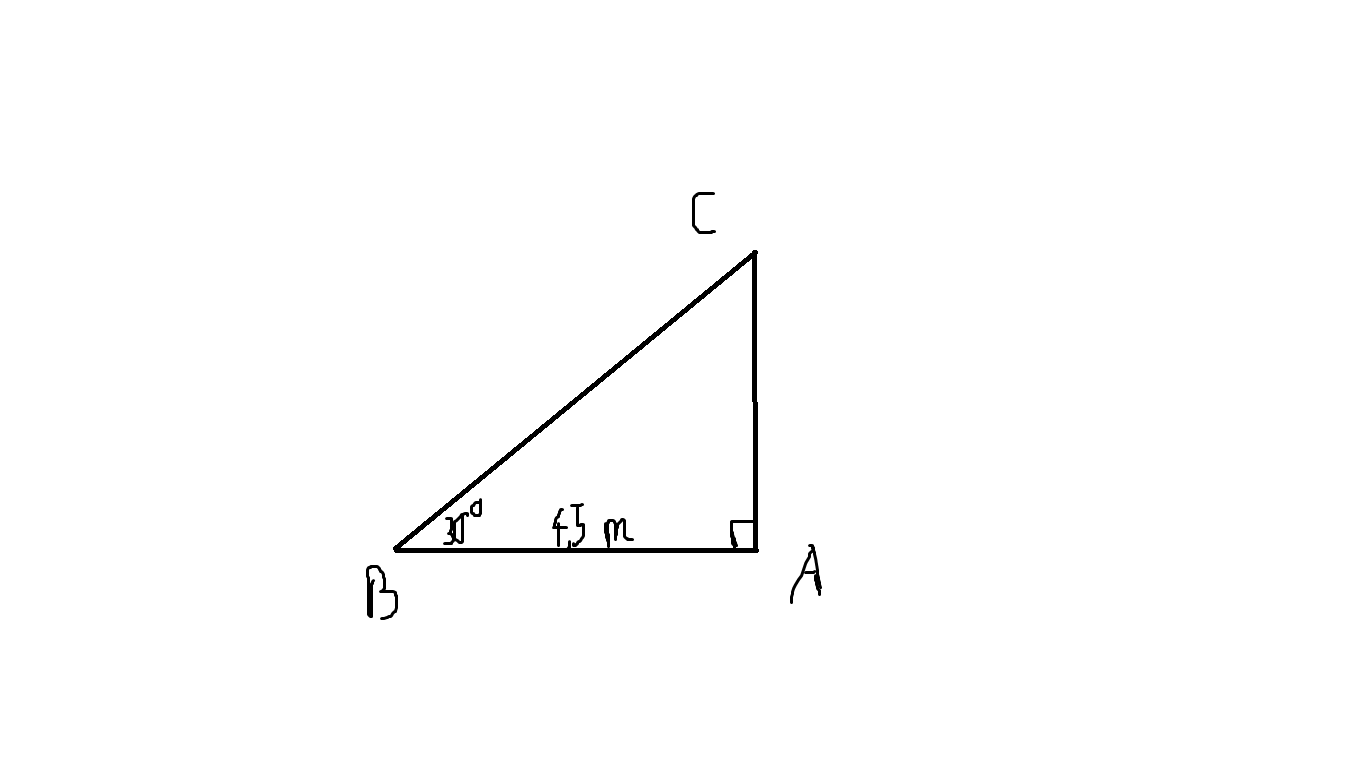
\(TanB=\dfrac{AC}{AB}\Rightarrow Tan30^o=\dfrac{AC}{4,5}\Rightarrow AC=Tan30^o.4,5=\dfrac{3\sqrt{3}}{2}\left(m\right)\)
\(CosB=\dfrac{AB}{BC}\Rightarrow Cos30^o=\dfrac{4,5}{BC}\Rightarrow BC=Cos30^o.4,5=\dfrac{9\sqrt{3}}{4}\)
Chiều cao ban đầu của cây tre là: \(\dfrac{3\sqrt{3}}{2}+\dfrac{9\sqrt{3}}{4}=\dfrac{15\sqrt{3}}{4}\approx6,5\left(m\right)\)

a)2 + 5 + 11 + ... + 47+ 95
Tính chất : 5 = 2.2 + 1
11 = 5.2 + 1
Vậy các số của dãy là: 2 + 5 + 7 + 11 + 23 + 47 + 95
= (2 + 5 + 7) + (5 + 95) + (23 + 47)
= 14 + 100 + 70
= 184


Câu 3:
2: Xét tứ giác OKEH có
\(\widehat{OKE}=\widehat{OHE}=\widehat{KOH}=90^0\)
Do đó: OKEH là hình chữ nhật
mà đường chéo OE là tia phân giác của \(\widehat{KOH}\)
nên OKEH là hình vuông
\(2.\)
\(a,1=\sqrt{1}\)
\(1< 2< =>\sqrt{1}< \sqrt{2}< =>1< \sqrt{2}\)
\(b,2-\sqrt{2}-1\)
\(1-\sqrt{2}\)
mà \(1< \sqrt{2}< =>1-\sqrt{2}< 0\)
\(2< \sqrt{2}+1\)
c, 7 và \(5\sqrt{2}\)
\(7=\sqrt{49}\)
\(5\sqrt{2}=\sqrt{50}< =>\sqrt{49}< \sqrt{50}\)
\(< =>7< 5\sqrt{2}\)
d, 7 và \(\sqrt{47}\)
\(7=\sqrt{49}< =>\sqrt{49}>\sqrt{47}\)
\(7>\sqrt{47}\)
e, 1 và \(\sqrt{3}-1\)
\(1-\sqrt{3}+1=2-\sqrt{3}=\sqrt{4}-\sqrt{3}>0\)
\(1>\sqrt{3}-1\)
f,\(2\sqrt{31}\)và \(10\)
\(2\sqrt{31}=\sqrt{124}\)
\(10=\sqrt{100}< =>\sqrt{124}>\sqrt{100}\)
\(2\sqrt{31}>10\)
\(3.A=\sqrt{1-4a+4a^2}-2a\)
\(A=\sqrt{\left(1-2a\right)^2}-2a\)
\(A=\left|1-2a\right|-2a\)
kết hợp với ĐKXĐ \(x\ge0,5\)
\(A=2a-1-2a=-1\)
\(b,B=\sqrt{x-2+2\sqrt{x-3}}\)
\(B=\sqrt{x-3+2\sqrt{x-3}+1}\)
\(B=\sqrt{\left(\sqrt{x-1}+1\right)^2}\)
\(B=\left|\sqrt{x-1}+1\right|\)
kết hợp đkxđ
\(B=\sqrt{x-1}+1\)
\(C=\sqrt{x-2\sqrt{x}+1}+\sqrt{x+2\sqrt{x}+1}\)
\(C=\sqrt{\left(\sqrt{x}-1\right)^2}+\sqrt{\left(\sqrt{x}+1\right)^2}\)
\(C=\left|\sqrt{x}-1\right|+\left|\sqrt{x}+1\right|\)
\(TH1:0\le x\le1\)
\(C=1-\sqrt{x}+\sqrt{x}+1=2\)
\(TH2:x>1\)
\(C=\sqrt{x}-1+\sqrt{x}+1=2\sqrt{x}\)
\(D=\sqrt{x-1+2\sqrt{x-1}+1}+\sqrt{x-1-2\sqrt{x-1}+1}\)
\(D=\sqrt{\left(\sqrt{x-1}+1\right)^2}+\sqrt{\left(\sqrt{x-1}-1\right)^2}\)
\(D=\left|\sqrt{x-1}+1\right|+\left|\sqrt{x-1}-1\right|\)
kết hợp với đkxđ
\(TH1:1\le x\le4\)
\(D=\sqrt{x-1}+1+1-\sqrt{x-1}=2\)
\(TH2:x>4\)
\(D=\sqrt{x-1}+1+\sqrt{x-1}+1=2\sqrt{x-1}\)