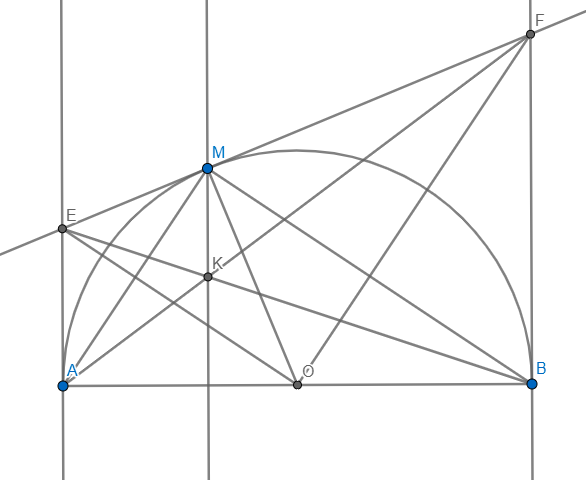
Cho nửa đường tròn (O) có đường kính AB = a. Gọi hai tia Ax, By là các tia vuông góc với AB ( Ax, By thuộc cùng một nửa mặt phẳng bờ AB). Qua một điểm M thuộc nửa đường tròn (O) (M không trùng với A và B), vẻ các tiếp tuyến với nửa đường tròn (O); chúng cắt Ax, By lần lượt tại 2 điểm E và F.
1. Chứng minh: EOF = 90o
2. Chứng minh tứ giác AEMO là một tứ giác nội tiếp; hai tam giác MAB và OEF đồng dạng.
3. Gọi K là giao của hai đường AF và BE, chứng minh rằng MK ⊥ AB.
4. Nếu MB = √3.MA, tính S tam giác KAB theo a.


Bài hơi khác 1 chút
Bạn tham khảo :
Hoặc bạn tìm ở phần câu hỏi tương tự