
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3: góc AMN=góic ACM
=>AM là tiếp tuyến của đường tròn ngoại tiếp ΔECM
=>góc AMB=90 độ
=>Tâm o1 của đường tròn ngoại tiếp ΔECM nằm trên BM
NO1 min khi NO1=d(N;BM)
=>NO1 vuông góc BM
Gọi O1 là chân đường vuông góc kẻ từ N xuống BM
=>O1 là tâm đường tròn ngoại tiếp ΔECM có bán kính là O1M
=>d(N;tâm đường tròn ngoại tiếp ΔECM) nhỏ nhất khi C là giao của (O1;O1M) với (O) với O1 ;là hình chiếu vuông góc của N trên BM



1 If I were Quang, I would study hard for the upcoming exam
2 The river in which the children prefer to swim is clean
3 The car which Mrs Brown has just bought is fast and modern
4 Mr Nick suggested changing the date of the meeting until next month
5 My nephew enjoyed feeding fish every morning
6 You won't pay much per month if you save energy
7 If the car weren't too expensive for us to buy
8 In spite of the heavy traffic, they got there in time
9 The movie which the kids were watching is interesting




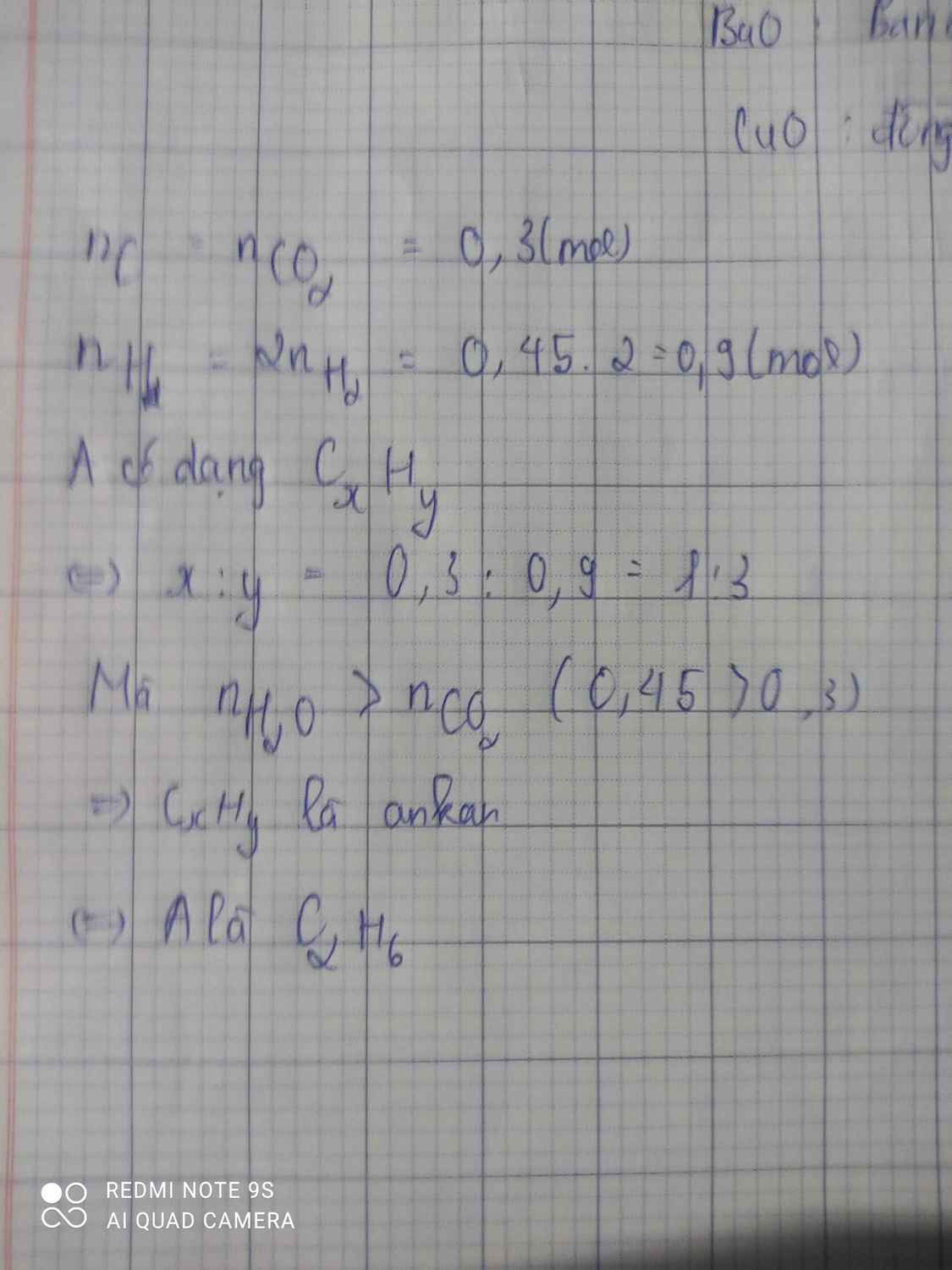
 ai giúp mình vs mình đang cần gấp
ai giúp mình vs mình đang cần gấp 
A B C M D E
a/
\(AD=\frac{AC}{2}\Rightarrow AD=CD\)
Xét tg AMD và tg CMD có chung đường cao từ M->AC và AD=CD nên \(S_{AMD}=S_{CMD}\)
Hai tg này có chung cạnh MD nên đường cao từ A->MD = đường cao từ C->MD
Xét tg AME và tg CME có chung ME và đường cao từ A->MD = đường cao từ C->MD nên \(S_{AME}=S_{CME}\)
b/
Xét tg ABC và tg EBC có chung đường cao từ C->AE và AB=BE nên \(S_{ABC}=S_{EBC}\)
Hai tg này có chung BC nên đường cao từ A->BC = đường cao từ E->BC
Xét tg AMC và tg CME có chung MC và đường cao từ A->BC = đường cao từ E->BC \(\Rightarrow S_{AMC}=S_{CME}\Rightarrow S_{AME}=S_{AMC}\)
Ta có \(AB=BE\Rightarrow\frac{AB}{AE}=\frac{1}{2}\)
Xét tg ABM và tg AME có chung đường cao từ M->AE và AB=BE nên
\(\frac{S_{ABM}}{S_{AME}}=\frac{AB}{AE}=\frac{1}{2}\Rightarrow\frac{S_{ABM}}{S_{AMC}}=\frac{1}{2}\)
Xét tg ABM và tg AMC có chung đường cao từ A->BC nên
\(\frac{S_{ABM}}{S_{AMC}}=\frac{MB}{MC}=\frac{1}{2}\Rightarrow MC=2xMB\)
c/
Ta có \(MB=3cm\Rightarrow MC=2xMB=2x3=6cm\)
\(BC=MB+MC=3+6=9cm\)
Ta có \(S_{ABC}=S_{EBC}\) mà \(S_{ABC}+S_{EBC}=S_{AEC}\Rightarrow S_{ABC}=S_{EBC}=\frac{S_{AEC}}{2}=\frac{36}{2}=18cm^2\)
\(S_{ABC}=\frac{BCxAH}{2}\Rightarrow AH=\frac{2xS_{ABC}}{BC}=\frac{2x18}{9}=4cm\)