Cứ 9 học sinh thì làm đc 72 tấm thiệp. Hỏi có 125 học sinh thì làm đc bao nhiêu tấm thiệp? (Các học sinh làm đc số tấm thiệp bằng nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 1
Gọi số bạn nam là x(bạn), số bạn nữ là y(bạn)
(Điều kiện: \(x,y\in Z^+\))
Lớp có 45 bạn nên x+y=45(1)
Số tấm thiệp các bạn nam làm được là 3x(tấm)
Số tấm thiệp các bạn nữ làm được là 2y(tấm)
Tổng số tấm thiệp cả lớp làm được là 115 tấm nên 3x+2y=115(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y=45\\3x+2y=115\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+3y=135\\3x+2y=115\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=20\\x+y=45\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=20\\x=25\end{matrix}\right.\left(nhận\right)\)
Vậy: Số bạn nam là 25 bạn
Số bạn nữ là 20 bạn
KV
23 tháng 1
Cách 2: giải bằng cách lập phương trình:
Gọi x (học sinh) là số học sinh nam của lớp 9A (x ∈ ℕ*)
Số học sinh nữ của lớp 9A là 45 - x (học sinh)
Số thiệp học sinh nam đã làm: 3x (tấm)
Số thiệp học sinh nữ đã làm: 2.(45 - x) (tấm)
Theo đề bài ta có phương trình:
3x + 2(45 - x) = 115
3x + 90 - 2x = 115
x = 115 - 90
x = 25 (nhận)
Vậy số học sinh nam của lớp 9A là 25 học sinh
Số học sinh nữ của lớp 9A là 45 - 25 = 20 học sinh
AH
Akai Haruma
Giáo viên
24 tháng 11 2021
Lời giải:
Gọi số tấm thiệp lớp 7A, 7B làm được lần lượt là $a,b$. Theo bài ra ta có:
Với năng suất như nhau, số tấm thiệp tỉ lệ thuận với số hs
$\Rightarrow \frac{a}{22}=\frac{b}{26}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{22}=\frac{b}{26}=\frac{a+b}{22+26}=\frac{24}{48}=\frac{1}{2}$
$\Rightarrow a=22.\frac{1}{2}=11; b=26.\frac{1}{2}=13$
AH
Akai Haruma
Giáo viên
24 tháng 11 2021
Bạn tham khảo lời giải tại đây:
https://hoc24.vn/cau-hoi/dechao-mung-ngay-nha-giao-viet-nam-hai-lop-7a-va-7b-lam-duoc-24-tam-thiep-tang-thay-co-biet-rang-lop-7a-co-22-hoc-sinh-lop-7b-co-26-hoc-sinh-hoi-moi-lop-lam-duoc-bao-nhieu-tam-thiep-giasurang-nan.3235937818385
7 tháng 3 2023
Gọi số tấm thiệp cần làm của lớp 7A,7B,7C lần lượt là a,b,c
Theo đề, ta có: a/15=b/14=c/11
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{a}{15}=\dfrac{b}{14}=\dfrac{c}{11}=\dfrac{a+b+c}{15+14+11}=1\)
=>a=15; b=14;c=11
24 tháng 9 2023
Tham khảo:
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên \(x \ge 0,y \ge 0\)
- Tổng số giờ vẽ không quá 30 giờ nên \(2x + 3y \le 30\)
- Số tấm thiệp tối thiểu là 12 tấm nên \(x + y \ge 12\)
Từ đó ta có hệ bất phương trình: \(\left\{ \begin{array}{l}2x + 3y \le 30\\x + y \ge 12\\x \ge 0\\y \ge 0\end{array} \right.(x,y \in \mathbb{N})\)
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ Oxy, ta được như hình dưới.
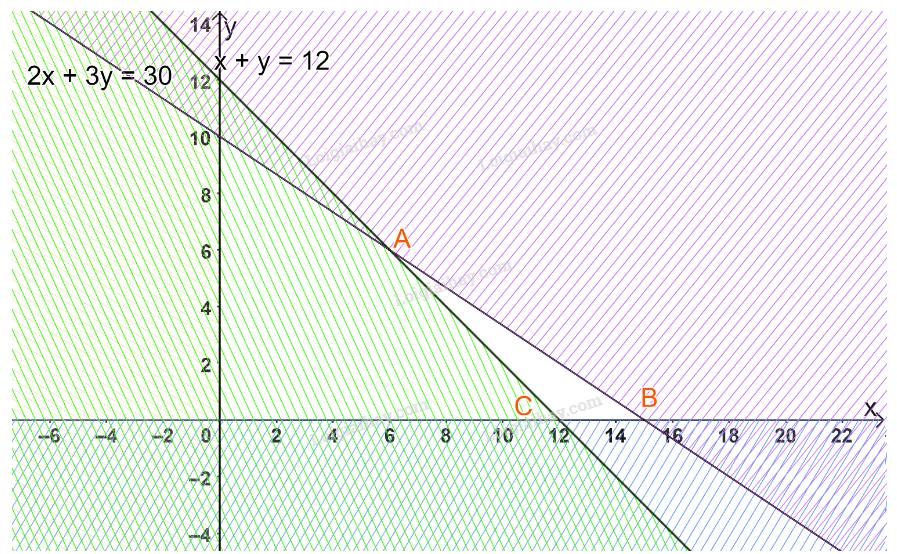
Miền không gạch chéo (miền tam giác ABC, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phương trình.
Với các đỉnh \(A(6;6),\)\(B(15;0),\)\(C(12;0).\)
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: \(F = 10x + 20y\)
Tính giá trị của F tại các đỉnh của tam giác:
Tại \(A(6;6):\)\(F = 10.6 + 20.6 = 180\)
Tại \(B(15;0):\)\(F = 10.15 + 20.0 = 150\)
Tại \(C(12;0):\)\(F = 10.12 + 20.0 = 120\)
F đạt giá trị lớn nhất bằng 180 tại \(A(6;6).\)
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất.
72:9=8 (học sinh )
125 × 8 = 1000 ( thiệp )
1 học sinh làm được số tấm thiếp là:
72:9=8 (học sinh)
125 học sinh làm được số tấm thiếp là:
8x125=1000 (tấm thiếp)
Đáp số:1000 tấm thiếp