\(\sqrt{49a^2}+3a\)Giúp mik nha mng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
19 tháng 7 2021
a) \(5\sqrt{25a^2}-25=25\left|a\right|-25==-25a-25\left(a< 0\right)\)
b) \(\sqrt{49a^2}+3a=7\left|a\right|+3a=-7a+3a\left(a< 0\right)=-4a\)
c) \(3\sqrt{9a^6}=9\left|a^3\right|-6a^3\)
Xét \(a\ge0\Rightarrow9\left|a^3\right|-6a^3=9a^3-6a^3=3a^3\)
Xét \(a< 0\Rightarrow9\left|a^3\right|-6a^3=-9a^3-6a^3=-15a^3\)
19 tháng 7 2021
a) 5\(\sqrt{25a^2}\) - 25 với a < 0
= 5\(\sqrt{\left(5a\right)^2}\) - 25
= 5.\(\left|5a\right|\) - 25
= 5.-(5a) - 25
= -25a - 25 Vì a < 0
b) \(\sqrt{49a^2}\) + 3a với a < 0
= \(\sqrt{\left(7a\right)^2}\) + 3a
= \(\left|7a\right|\) + 3a
= -7a + 3a Vì a < 0
= -4a
c) 3\(\sqrt{9a^6}\) - 6a3 với a bất kì
= 3\(\sqrt{\left(3a^3\right)^2}\) - 6a3
= 3\(\left|3a^3\right|\) - 6a3
= 9a3 - 6a3
= 3a3
Chúc bạn học tốt
N
3
16 tháng 4 2023
IX
2. j
3. i
4. f
5. c
6. a
7. h
8. e
9. g
10. d
XI
2. part => parts
3. a => an
4. a => an
5. a => the
6. are => will be (không chắc lắm)
7. taking => take
8. are => is
C.
Bài 1
1. C
2. B
3. C
4. B
(Nên double-check trước khi chép)
10 tháng 9 2021
\(49a^2-\left(3a-b\right)^2=\left(7a-3a+b\right)\left(7a+3a-b\right)=\left(4a+b\right)\left(10a-b\right)\)
31 tháng 7 2023
b: B=căn 49a^2+3a
=|7a|+3a
=7a+3a(a>=0)
=10a
c: C=căn16a^4+6a^2
=4a^2+6a^2
=10a^2
d: \(D=3\cdot3\cdot\sqrt{a^6}-6a^3=6\cdot\left|a^3\right|-6a^3\)
TH1: a>=0
D=6a^3-6a^3=0
TH2: a<0
D=-6a^3-6a^3=-12a^3
e: \(E=3\sqrt{9a^6}-6a^3\)
\(=3\cdot\sqrt{\left(3a^3\right)^2}-6a^3\)
=3*3a^3-6a^3(a>=0)
=3a^3
f: \(F=\sqrt{16a^{10}}+6a^5\)
\(=\sqrt{\left(4a^5\right)^2}+6a^5\)
=-4a^5+6a^5(a<=0)
=2a^5
TA
1
Y
2 tháng 7 2023
\(\sqrt{x^2-4}-x+2=0\\ \Leftrightarrow\sqrt{x^2-4}=x-2\\ \Leftrightarrow\left(\sqrt{x^2-4}\right)^2=\left(x-2\right)^2\)
\(\Leftrightarrow x^2-4-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)^2=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-x+2\right)=0\)
\(\Leftrightarrow\left(x-2\right)4=0\)
\(\Leftrightarrow x=2\)
Vậy \(S=\left\{2\right\}\)
DM
5
KV
18 tháng 8 2023
Bài 2
a) x/8 = 5,4/3
x = 8 . 5,4/3
x = 14,4
b) 2,5 : 7,5 = x : 3/5
x = 3/5 × 1/3
x = 1/5
c) 2 2/3 : x = 1 7/9 : 0,2
8/3 : x = 16/9 : 1/5
x = 8/3 : (16/9 : 1/5)
x = 8/3 : 80/9
x = 3/10
d) 4/x = x/0,16
x² = 4 . 0,16
x² = 0,64
x = 0,8 hoặc x = -0,8
KV
18 tháng 8 2023
Bài 3
a) x/9 = y/11 và x + y = 60
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
x/9 + y/11 = (x + y)/(9 + 11) = 60/20 = 3
x/9 = 3 ⇒ x = 9.3 = 27
y/11 = 3 ⇒ y = 11.3 = 33
Vậy x = 27; y = 33
b) x/3 = y/5 ⇒ 2x/6 = y/5 và 2x - y = 8
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
2x/6 = y/5 = (2x - y)/(6 - 5) = 8/1 = 8
2x/6 = 8 ⇒ x = 6.8:2 = 24
y/5 = 8 ⇒ y = 5.8 = 40
Vậy x = 24; y = 40
c) 7x = 4y ⇒ y/7 = x/4 và y - x = 24
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
y/7 = x/4 = (y - x)/(7 - 4) = 24/3 = 8
x/4 = 8 ⇒ x = 4.8 = 32
y/7 = 8 ⇒ y = 7.8 = 56
Vậy x = 32; y = 56
P7
1
14 tháng 10 2021
1. a) mẹ
b) thân mẫu
2. a) phu nhân
b) vợ
3. a) chết, lâm chung
b) lâm chung
4. a) giáo huấn
b) dạy bảo
AH
Akai Haruma
Giáo viên
12 tháng 8 2023
Lời giải:
a. Với $n$ nguyên khác -3, để $B$ nguyên thì:
$2n+9\vdots n+3$
$\Rightarrow 2(n+3)+3\vdots n+3$
$\Rightarrow 3\vdots n+3$
$\Rightarrow n+3\in\left\{\pm 1; \pm 3\right\}$
$\Rightarrow n\in\left\{-2; -4; 0; -6\right\}$
b.
$B=\frac{2n+9}{n+3}=\frac{2(n+3)+3}{n+3}=2+\frac{3}{n+3}$
Để $B_{\max}$ thì $\frac{3}{n+3}$ max
Điều này đạt được khi $n+3$ là số nguyên dương nhỏ nhất
Tức là $n+3=1$
$\Leftrightarrow n=-2$
c. Để $B$ min thì $\frac{3}{n+3}$ min
Điều này đạt được khi $n+3$ là số nguyên âm lớn nhất
Tức là $n+3=-1$
$\Leftrightarrow n=-4$
H9
HT.Phong (9A5)
CTVHS
1 tháng 7 2023
1) \(\sqrt{x^2-x}=x\)
\(\Leftrightarrow x^2+x=x^2\)
\(\Leftrightarrow x^2+x-x^2=0\)
\(\Leftrightarrow x=0\)
Vậy: \(x=0\)
2) \(\sqrt{1-x^2}=x-1\) (ĐK: \(x\le1\))
\(\Leftrightarrow1-x^2=\left(x-1\right)^2\)
\(\Leftrightarrow1-x^2=x^2-2x+1\)
\(\Leftrightarrow-x^2-x^2-2x=1-1\)
\(\Leftrightarrow-2x^2-2x=0\)
\(\Leftrightarrow-2x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=-1\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;-1\right\}\)
1 tháng 7 2023
1: =>x^2+x=x^2 và x>=0
=>x=0
2: =>1-x^2=x^2-2x+1 và x>=1
=>x^2-2x+1-1+x^2>=0 và x>=1
=>2x^2-2x=0 và x>=1
=>x=1
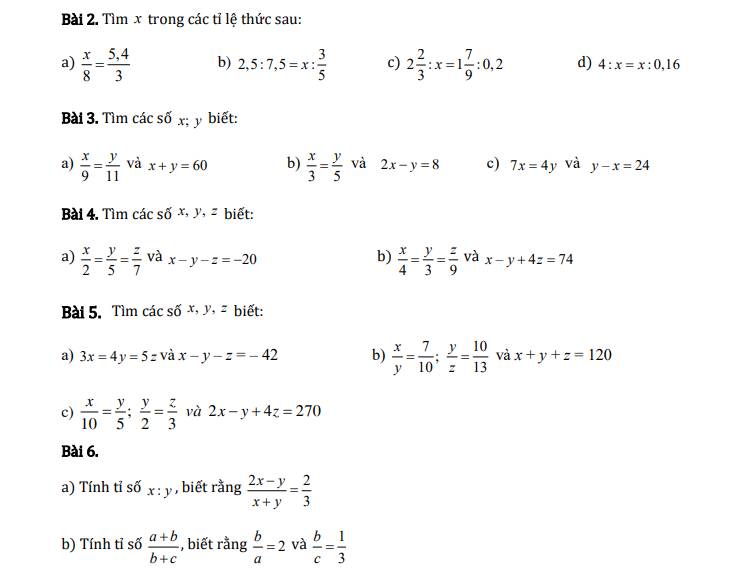
\(\sqrt{49a^2}+3a\)
\(\sqrt{49}\sqrt{a^2}+3a\)
\(7a+3a\)
\(=10a\)