Giúp vs ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TP
1
mk vs ạ
8 tháng 8 2023
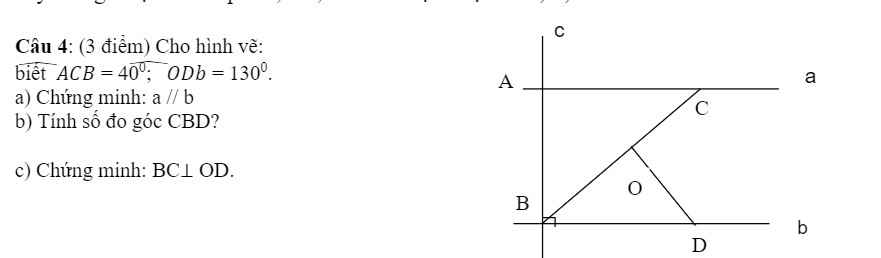
Mình xin phép bổ sung một chút vào trong hình vẽ nha bạn. Chứ để như vậy thì ko chứng minh a song song với b đâu
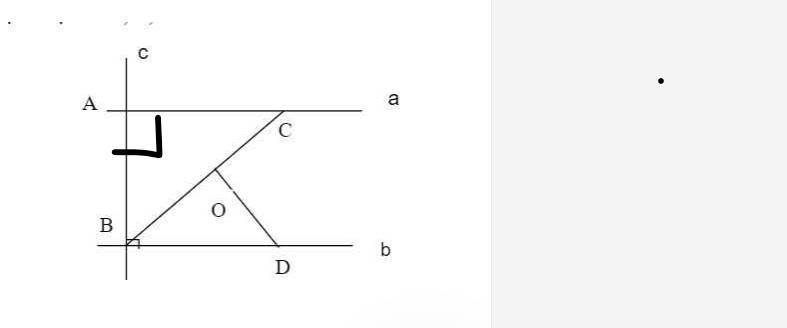
a: a vuông góc AB
b vuông góc AB
=>a//b
b: a//b
=>góc ACB=góc CBD
=>góc CBD=40 độ
c: góc ODB=180-130=50 độ
góc ODB+góc OBD=50+40=90 độ
=>ΔOBD vuông tại O
=>DO vuông góc BC
gấp mn giúp em câu này vs ạ e gấp lắm mn giúp em vs em cảm ơn ạ
10 tháng 1 2022
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
19 tháng 6 2023
a: CH=16^2/24=256/24=32/3(cm)
BC=24+32/3=104/3cm
AC=căn 32/3*104/3=16/3*căn 13(cm)
b: BC=12^2/6=144/6=24cm
CH=24-6=18cm
AC=căn 18*24=12*căn 3(cm)
KL
1
7 tháng 1 2022
5: Để A nguyên thì \(x^2-4+6⋮x+2\)
\(\Leftrightarrow x+2\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)
hay \(x\in\left\{-1;-3;0;-4;1;-5;4;-8\right\}\)
PL
3
NN
6
HT
2
PL
1
A B C H
a) Xét t/giác ABC và t/giác HBA
có: \(\widehat{BAC}=\widehat{BHA}=90^0\)
\(\widehat{B}\): chung
=> t/giác ABC đồng dạng t/giác HBA (g.g)
=> AB/HB = BC/AB => AB2 = BC.HB
b) Xét t/giác AHB và t/giác CHA
có: \(\widehat{BHA}=\widehat{AHC}=90^0\)(gt)
\(\widehat{B}=\widehat{HAC}\)(cùng phụ \(\widehat{C}\))
=> t/giác AHB đồng dạng t/giác CHA (g.g)
=> AH/CH = HB/AH => AH2 = HB.HC
Xét t/giác AHC và t/giác BAC
có \(\widehat{AHC}=\widehat{BAC}=90^0\)(gt)
\(\widehat{C}\) : chung
=> t/giác AHC đồng dạng t/giác BAC (g.g)
=> AC/BC = HC/AC => AC2 = BC.HC
c) Xét t/giác ABC vuông tại A => BC2 = AB2 + AC2 (Pi - ta - go)
=> BC2 = 62 + 82 = 100 => BC = 10
Ta có: SABC = 1/2AB.AC = 1/2AH.BC
=> AH = AB.AC/BC = 6.8/10 = 4,8
Do AB2 = BH.BC (cm câu a) => BH = 62/10 = 3,6
Vậy ...