Cho tam giácABC có 3 góc nhọn nội tiếp đường tròn (O).Các đường cao AD BE CF cắt nhau tại H. CMR:
AE .AC=AH.AD=AF.AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
DO đó: ΔABE\(\sim\)ΔACF
SUy ra: AB/AC=AE/AF
hay \(AB\cdot AF=AE\cdot AC\)
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc EAF chung
Do đó: ΔAEF\(\sim\)ΔABC
Suy ra: \(\widehat{AEF}=\widehat{ABC}\)

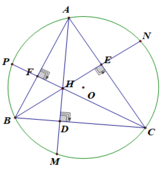
c) Xét ΔAEH và ΔADC có:
∠(AEH) = ∠(ADC) = 90 0
∠(DAC) là góc chung
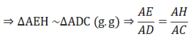
⇒ AE.AC = AD.AH
Xét Δ BEC và ΔADC có:
∠(BEC) = ∠(ADC) = 90 0
∠(ACD) là góc chung
⇒ ΔBEC ∼ ΔADC (g.g)
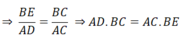

a: Xét tứ giác BFEC có
\(\widehat{BFC}=\widehat{BEC}=90^0\)
=>BFEC là tứ giác nội tiếp
=>B,F,E,C cùng thuộc một đường tròn
b: Xét ΔAHE vuông tại E và ΔACD vuông tại D có
\(\widehat{HAE}\) chung
Do đó: ΔAHE đồng dạng với ΔACD
=>\(\dfrac{AH}{AC}=\dfrac{AE}{AD}\)
=>\(AH\cdot AD=AC\cdot AE\)
Xét ΔABC có AD là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot AD\cdot BC\left(1\right)\)
Xét ΔABC có BE là đường cao
nên \(S_{ABC}=\dfrac{1}{2}\cdot BE\cdot AC\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{1}{2}\cdot AD\cdot BC=\dfrac{1}{2}\cdot BE\cdot AC\)
=>\(AD\cdot BC=BE\cdot AC\)

a: góc BDH+góc BFH=180 độ
=>BDHF nội tiếp
góc BFC=góc BEC=90 dộ
=>BFEC nội tiếp
b: góc FEB=góc BAD
góc DEB=góc FCB
mà góc BAD=góc FCB
nên góc FEB=góc DEB
=>EB là phân giác của góc FED
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc OA
=>OA vuông góc IK