Cho tam giác ABC vuông tại A, đường cao AH. Biết rằng AB=6cm và AC=8cm. Tính độ dài AH, BH, CH, và BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 12 2021
\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)
VN
23 tháng 1 2017
Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
VN
23 tháng 1 2017
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC
CM
30 tháng 9 2018
a, HB = 1,8cm; CH = 3,2cm; AH = 2,4cm; AC = 4cm
b, AB = 65cm; AC = 156cm; BC = 169cm; BH = 25cm
c, AB = 5cm; BC = 13cm; BH = 25/13cm; CH = 144/13cm
2 tháng 10 2021
a) Các hệ thức giữa cạnh và đường cao AH:
\(AH^2=BH.CH\)
\(AB^2=BH.BC\)
\(AC^2=CH.BC\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(AH.BC=AB.AC\)
b) Áp dụng HTL trong tam giác ABC vuông tại A có đg cao AH:
\(AH.BC=AB.AC\)
\(\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4,8\left(cm\right)\)
Ta có: \(AB^2=BH.BC\)
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\left(cm\right)\)
\(BC=CH+BH\)
\(\Rightarrow CH=BC-BH=10-3,6=6,4\left(cm\right)\)
MH
12 tháng 5 2022
(Tự vẽ hình)
a) Xét \(\Delta AHB\) và \(\Delta CAB\) có:
\(\widehat{AHB}=\widehat{CAB}=90^0\)
\(\widehat{B}\) chung
\(\Rightarrow\Delta AHB\sim\Delta CAB\) (g.g)
b) Áp dụng định lý Pytago có:
\(BC^2=AB^2+AC^2=8^2+6^2=100\Rightarrow BC=10\left(cm\right)\)
Do \(\Delta AHB\sim\Delta CAB\Rightarrow\left\{{}\begin{matrix}\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{AB.AC}{BC}=4,8\left(cm\right)\\\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\end{matrix}\right.\)
c) Xét \(\Delta AHB\) và \(\Delta CHA\) có:
\(\widehat{AHB}=\widehat{CHA}=90^0\)
\(\widehat{ABH}=\widehat{CAH}\) (cùng phụ \(\widehat{BAH}\))
\(\Rightarrow\Delta AHB\sim\Delta CHA\) (g.g) \(\Rightarrow\dfrac{AH}{BH}=\dfrac{CH}{AH}\Rightarrow AH^2=BH.CH\)
2 tháng 8 2021
Bài 1:
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH=\dfrac{9^2}{15}=\dfrac{81}{15}=5.4\left(cm\right)\)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=15-5,4=9,6(cm)
b) Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=1+3=4(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC=1\cdot4=4\left(cm\right)\\AC^2=CH\cdot BC=3\cdot4=12\left(cm\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=2\left(cm\right)\\AC=2\sqrt{3}\left(cm\right)\end{matrix}\right.\)
KV
25 tháng 4 2023
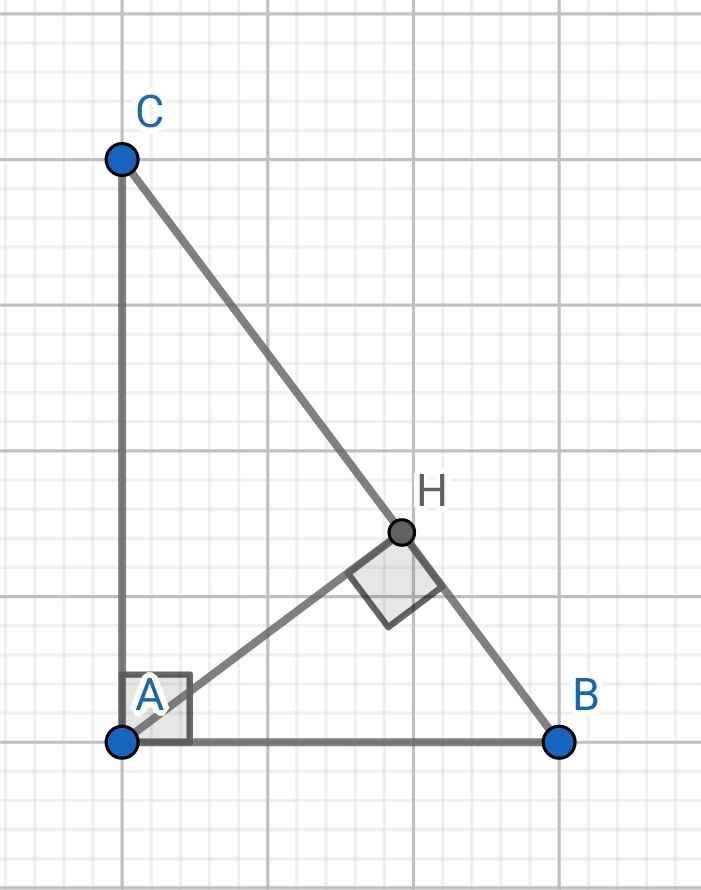
a) Xét hai tam giác vuông: ∆ABC và ∆HBA có:
∠B chung
⇒ ∆ABC ∽ ∆HBA (g-g)
b) ∆ABC vuông tại A (gt)
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10
Do ∆ABC ∽ ∆HBA (cmt)
⇒ AC/AH = BC/AB
⇒ AH = AB.AC/BC
= 6.8/10
= 4,8 (cm)
∆ABH vuông tại H
⇒ AB² = AH² + BH² (Pytago)
⇒ BH² = AB² - AH²
= 6² - (4,8)²
= 12,96
⇒ BH = 3,6 (cm)
CH
25 tháng 4 2023
a) Ta có:
- Góc A của tam giác ABC là góc vuông, nên ta có thể tính được độ dài đoạn thẳng AH bằng cách sử dụng định lí Pythagoras: AH = sqrt(AB^2 + AC^2) = sqrt(6^2 + 8^2) = 10.
- Góc A của tam giác ABC cũng là góc giữa đường cao AH và cạnh huyền BC, nên ta có thể tính được tỉ số giữa độ dài đoạn thẳng AH và độ dài cạnh huyền BC: AH/BC = AC/AB = 8/6 = 4/3.
- Từ tỉ số này, ta có thể suy ra rằng tam giác ABC đồng dạng với tam giác HBA (vì cả hai tam giác có cùng một góc và tỉ số giữa các cạnh tương ứng bằng nhau).
b) Để tính độ dài các cạnh BC, AH, BH, ta có thể sử dụng các công thức sau:
- Độ dài cạnh BC: BC = AB/AC * AH = 6/8 * 10 = 15/2 = 7.5.
- Độ dài đoạn thẳng BH: BH = sqrt(AH^2 - AB^2) = sqrt(10^2 - 6^2) = 8.
- Độ dài đoạn thẳng AH đã được tính ở trên: AH = 10.
Vậy độ dài các cạnh BC, AH, BH lần lượt là 7.5cm, 10cm, 8cm.
AH
Akai Haruma
Giáo viên
9 tháng 10 2021
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AB^2=BH.BC$
$\Rightarrow BH=\frac{AB^2}{BC}=\frac{6^2}{10}=3,6$ (cm)
$CH=BC-BH=10-3,6=6,4$ (cm)
Tiếp tục áp dụng HTL:
$AH^2=BH.CH=3,6.6,4$
$\Rightarrow AH=4,8$ (cm)
$AC^2=CH.BC=6,4.10=64$
$\Rightarrow AC=8$ (cm)
AH
Akai Haruma
Giáo viên
9 tháng 10 2021
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+1^2}=2$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{\sqrt{3}.1}{2}=\frac{\sqrt{3}}{2}$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{3-\frac{3}{4}}=\frac{3}{2}$ (cm)
$CH=BC-BH=2-\frac{3}{2}=\frac{1}{2}$ (cm)
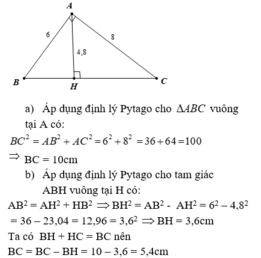
Diện tích tam giác ABC là:
6.8:2=24 (cm2)
Áp dụng định lí Py-ta-go cho tam giác ABC, ta có:
AB2+AC2=BC2
=>62+82=BC2=>36+64=BC2=>BC=10 (cm)
Đường cao AH dài là:
24.2:10=4,8 (cm)
Áp dụng định lí Py-ta-go cho tam giác ABH, ta có:
AH2+BH2=AB2
=>4,82+BH2=36
=>23,04+BH2=36
=>BH2=12,96=>BH=3,6 (cm)
Độ dài CH là:
10-3,6=6,4 (cm)
Đáp số: AH: 4,8 cm; BH: 3,6 cm; CH: 6,4 cm; BC: 10 cm
\(\text{Áp dụng định lý Pytago ta có:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC^2=6^2+8^2\)
\(\Rightarrow BC^2=100\)
\(\Rightarrow BC=10\left(\text{Vì BC}>0\right)\)
\(S_{\Delta ABC}\text{ là}:\)
\(\frac{6.8}{2}=24\)
\(\text{Vì AH là đường cao hạ từ đỉnh A và BC là đáy tương ứng với đường cao AH nên}\)
\(S_{\Delta ABC}=\frac{BC.AH}{2}=\frac{10.AH}{2}=24\)
\(\Rightarrow AH=24:5=4,8\)
\(\text{Áp dụng định lý Pytago ta có:}\)
\(AB^2=AH^2+BH^2\)
\(\Rightarrow6^2=4,8^2+BH^2\)
\(BH^2=12.96\)
\(BH=3,6\)
\(\text{CH thì tính tương tự như BH nha}\)