Cho 2 đoạn thẳng AB và CD cắt nhau tại 2 trung điểm của đoạn thẳng. Gọi M và N lần lượt là trung điểm của AD và BD. CM và CN cắt AB theo thứ tự tại E và F. CMR: AE = EF = FB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


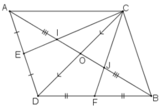
Gọi O là giao điểm của hai đoạn thẳng AB và CD.
⇒ AO = OB và CO = OD.
+ ΔACD có trung tuyến AO, CE cắt nhau tại I
⇒ I là trọng tâm ΔACD
⇒ AI = 2/3. AO = 2/3. 1/2. AB = 1/3.AB
+ Tương tự J là trọng tâm ΔBCD
⇒ BJ = 2/3. BO = 2/3. 1/2. BA = 1/3.AB
⇒ IJ = AB – AI – BJ = 1/3.AB
Vậy AI = IJ = JB

Hình bên dưới nha.
Giải thích các bước giải:
M;N lần lượt là trung điểm của AD,BCM;N lần lượt là trung điểm của AD,BC
⇒MN là đường trung bình của hình thang ABCD⇒MN là đường trung bình của hình thang ABCD
⇒MN=2+52=3,5;MN//AB//CD⇒MN=2+52=3,5;MN//AB//CD
MN//AB⇒ME//AB mà M là trung điểm ABMN//AB⇒ME//AB mà M là trung điểm AB
⇒ME là đường trung bình của ΔABD⇒ME là đường trung bình của ΔABD
⇒ME=AB2=1⇒ME=AB2=1
:Chứng minh tương tự:NF là đường trung bình của ΔACB:Chứng minh tương tự:NF là đường trung bình của ΔACB
⇒NF=AB2=1⇒NF=AB2=1
⇒EF=MN−ME−MF=3,5−1−1=1,5⇒EF=MN−ME−MF=3,5−1−1=1,5
Vậy EF=1,5Vậy EF=1,5

Ta có:
a) \(F=-\frac{1}{2}x^2-2x-6=-\frac{1}{2}\left(x^2+4x+4\right)-4\)
\(=-\frac{1}{2}\left(x+2\right)^2-4\le-4< 0\left(\forall x\right)\)
=> F luôn âm với mọi x
b) \(G=\left(x-1\right)\left(x+2\right)-5=x^2+x-2-5\)
\(=x^2+x-7=\left(x^2+x+\frac{1}{4}\right)-7-\frac{1}{4}=\left(x+\frac{1}{2}\right)^2-\frac{29}{4}\)
Ko thể xác định G luôn âm hay dương

Gọi O là giao điểm của AB và CD
=>O là trung điểm chng của AB và CD
Xét ΔACD có
AO là đường trung tuyến
CE là đường trung tuyến
AO cắt CE tại I
Do đó: I là trọng tâm
=>AI=2/3AO=1/3AB(1)
Xét ΔCBD có
BO là đường trung tuyến
CF là đường trung tuyến
BO cắt CF tại J
Do đó; J là trọng tâm
=>BJ=2/3BO=1/3BA(2)
Từ (1) và (2) suy ra AI=BJ=1/3AB=JI

a)
ta có: ABCD là hình vuông
=> AB=BC=CD=DA=>1/2AB=1/2CD=AI=JC
AI//JC
=>tứ giác AICJ là hình bình hành
gọi trung điểm của AC là K
ta có:ABCD là hình vuông=> AC và BD cắt nhau tại trung điểm của mỗi đường
=>BD cắt AC tại K(1)
ta có AICJ là hình bình hành => AC và DJ cắt nhau tại trung điểm của mỗi đường
=>DJ cắt AC tại K(2)
từ (1)(2)=> 3 đoạn thẳng AC,BD,Ị cắt nhau tại trung điểm K của chúng
b)
ta có:
góc ADB=góc DBC
AJ//IC=> góc AED=góc CFB
ta có:
\(\widehat{EAD}=180^o-\widehat{ADB}-\widehat{AED}\)
\(\widehat{FCB}=180^o-\widehat{DBC}-\widehat{CFB}\)
=>góc EAD=góc FCB
xét tam giác DEA và tam giác BFC có
AD=BC(gt)
góc ADB=góc DBC
góc EAD=góc FCB(cmt)
=>tam giác DEA=tam giác BFC(g.c.g)
=>AE=CF
c)
ta có:tứ giác AICJ là hình bình hành
=>AJ=IC
AE=CF
EJ=AJ-AE
IF=IC-FC
=>EJ=IF
EJ//IF
=>tứ giác IFJE là hình bình hành
d)
xét tam giác ACD có
DK là trung tuyến ứng với cạnh AC
AJ là trung tuyến ứng với cạnh CD
=>giao của DK và AJ là trọng tâm tam giác ACD
=>E là trọng tâm tam giác ACD
cm tương tự ta có: F là trọng tâm tam giác ABC
ta có:
E là trọng tâm tam giác ADC
=>EK=1/2DE
F là trọng tâm tam giác ABC
=>FK=1/2BF
DE=BF(tam giác DEA=tam giác BFC)
=>EK=FK
ta có:
=>FB= DE=2EK=EK+KF=EF
=>DE=EF=FB(đfcm)
