Cho hàm số \(y=\frac{x^2+ax+b}{x^2+1}\), tìm a, b sao cho hàm số có miền giá trị là [-1;9]
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
22 tháng 8 2023
a) Để tìm giá trị của b, ta thay x = 2 vào phương trình y = -3x + b - 3x^2 + c. Vì y = 1, ta có:
1 = -3(2) + b - 3(2)^2 + c 1 = -6 + b - 12 + c 1 = b + c - 18
Đồng thời, ta biết rằng đồ thị của hàm số đi qua điểm (2, 1), vì vậy ta có thêm một điều kiện:
1 = -3(2) + b - 3(2)^2 + c 1 = -6 + b - 12 + c 1 = b + c - 18
Từ hai phương trình trên, ta có thể giải hệ phương trình để tìm giá trị của b.
b) Để tìm a và b, ta sử dụng hai điểm A(2, 3) và B(1, 1) để lập hệ phương trình:
3 = a(2) + b(2)^2 + c 1 = a(1) + b(1)^2 + c
Từ đó, ta có thể giải hệ phương trình để tìm giá trị của a và b.
Sau khi tìm được giá trị của a và b, ta có thể vẽ đồ thị của hàm số y = ax + b + c.
9 tháng 1 2024
Bài 2:
a: Thay x=1 và y=1 vào y=ax+5, ta được:
\(a\cdot1+5=1\)
=>a+5=1
=>a=-4
b: a=-4 nên y=-4x+5
| x | -2 | -1 | 0 | 1/2 | -3 |
| y=-4x+5 | 13 | 9 | 5 | 3 | -7 |
Bài 1:
a: \(y=-2\left(x+5\right)-4\)
\(=-2x-10-4\)
=-2x-14
a=-2; b=-14
b: \(y=\dfrac{1+x}{2}\)
=>\(y=\dfrac{1}{2}x+\dfrac{1}{2}\)
=>\(a=\dfrac{1}{2};b=\dfrac{1}{2}\)
4 tháng 6 2017
Câu 1: để hàm số có đồ thị hàm số đi qua điểm A và B nên tọa độ của A,B thỏa mãn đồ thị nên ta có hệ
\(\hept{\begin{cases}-2a+b=5\\a+b=-4\end{cases}\Leftrightarrow}\hept{\begin{cases}a=-3\\b=-1\end{cases}}\)
Câu 2 :
- để hàm số luôn nghịch biến thì hệ số góc của đường thẳng nhỏ hơn 0 nên : \(2m-1< 0\Leftrightarrow m< \frac{1}{2}\)
- Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(\frac{-2}{3}\)tức giao điểm có tọa độ \(\left(-\frac{2}{3};0\right)\)nên có phương trình :\(0=\frac{-2\left(2m-1\right)}{3}+m+2\Leftrightarrow-4m+2+3m+6=0\Leftrightarrow m=8\)
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
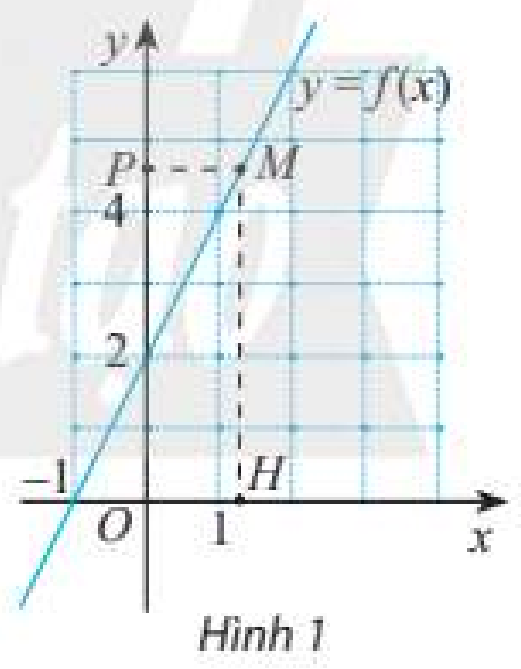
a) Khi \(x\) càng gần đến 1 thì giá trị của hàm số càng gần đến 4.
b) Khi điểm \(H\) thay đổi gần về điểm \(\left( {1;0} \right)\) trên trục hoành thì điểm \(P\) càng gần đến điểm \(\left( {0;4} \right)\).