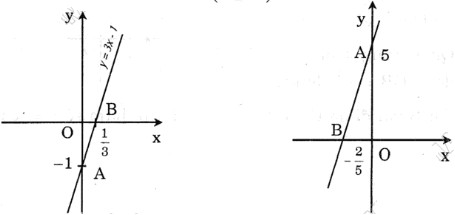Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: để hàm số có đồ thị hàm số đi qua điểm A và B nên tọa độ của A,B thỏa mãn đồ thị nên ta có hệ
\(\hept{\begin{cases}-2a+b=5\\a+b=-4\end{cases}\Leftrightarrow}\hept{\begin{cases}a=-3\\b=-1\end{cases}}\)
Câu 2 :
- để hàm số luôn nghịch biến thì hệ số góc của đường thẳng nhỏ hơn 0 nên : \(2m-1< 0\Leftrightarrow m< \frac{1}{2}\)
- Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \(\frac{-2}{3}\)tức giao điểm có tọa độ \(\left(-\frac{2}{3};0\right)\)nên có phương trình :\(0=\frac{-2\left(2m-1\right)}{3}+m+2\Leftrightarrow-4m+2+3m+6=0\Leftrightarrow m=8\)

a, Bạn xem lại cách vẽ parabol rồi tự vẽ hình nhé
b, C thuộc vào P nên :
\(m=\frac{1}{2}.\left(-2\right)^2=2\)

a)
đường thẳng (d1) song song với đường thẳng (d2) khi :
a = a' và b khác b'
suy ra :
\(m-1=3\) \(\Leftrightarrow m=4\)
vậy đường thẳng (d1) song song với đường thẳng (d2) khi m = 4

Bài giải:
a) Thế x = 4 và y = 11 vào y = 3x +b ta có: 11 = 3.4 + b ⇔ b = -1. Khi đó hàm số đã cho trở thành: y = 3x – 1. Đây là đường thẳng đi qua 2 điểm A(0;-1) và B(1/3; 0)
b) Đồ thị hàm số y = ax + 5 đi qua điểm A(-1; 3) nên: 3 = a(-1) + 5
<=> a = 2
Khi đó hàm số đã cho trở thành : y = 2x + 5. Đây là đường thẳng đi qua hai điểm A(0; 5) và B (−52;0)(−52;0)